Assume we have an antenna with a radiation resistance of 10
 , an antenna current of 2A and a gain of 4 (6dB). This antenna will radiate a power of 10 x 22 x 4 = 160 Watt.
, an antenna current of 2A and a gain of 4 (6dB). This antenna will radiate a power of 10 x 22 x 4 = 160 Watt.Antennas for 136kHz
About this page :
The main object of this page is to provide information. It has been deliberately kept simple, no fancy and flashy tricks, in order to achieve maximum compatibility for the different browsers and to allow fast downloading.
Any comments and/or suggestions are welcome at : on7yd@uba.be
A Japanese translation of this page, by Susumu Morioka (JH1GVY), is available here
last updated on 30 January 2009
Index
The main subject will be transmitting antennas for 136kHz as this often is the most important part of a longwave amateur radio station. The aim of the transmitting antenna is to radiate the power coming from the transmitter.
The power radiated by any antenna is determined by 3 factors :
Example :
Assume we have an antenna with a radiation resistance of 10 , an antenna current of 2A and a gain of 4 (6dB). This antenna will radiate a power of 10 x 22 x 4 = 160 Watt.
, an antenna current of 2A and a gain of 4 (6dB). This antenna will radiate a power of 10 x 22 x 4 = 160 Watt.
The gain of an antenna is always given relative to a reference antenna. Most common references are the 1/2 wave dipole and the isotropic radiator. This last is a virtual antenna that has no directivity at all, it radiates equally to all directions. In general the gain of any antenna relative to a 1/2 wave dipole is given as dBd while the gain relative to an isotropic radiator is given as dBi. Due to its directivity a 1/2 wave dipole has a gain 1.64 relative to a isotropic radiator (2.15dBi).
At first sight the radiation resistance of an antenna has no influence on the radiated power, as long as you match your transmitter to this resistance. But unfortunately the radiation resistance is not the only resistance that is consuming the transmitter power, there are also the loss resistances. These losses occur within the antenna (+ the antenna matching system) and in the environment of the antenna (ground, objects near the antenna). On HF these loss resistances are often negligible as they are rather small compared to the radiation resistance, but on longwave this is certainly not the case. For most longwave antennas used by amateurs the radiation resistance of the antenna is in the range of 10 to a few hundred m while loss resistances are in the range of 30 to 150
while loss resistances are in the range of 30 to 150 . This means that, dependent on the antenna and its environment, about 99% to 99.99% of the transmitter power is not radiated but absorbed in the loss resistances.
. This means that, dependent on the antenna and its environment, about 99% to 99.99% of the transmitter power is not radiated but absorbed in the loss resistances.
The two most common transmitting antennas on longwave are the short vertical monopole (Marconi antenna) and the small loop antenna. The short vertical monopole is an electric antenna, it creates an electric field 'on the spot' (near the antenna) while the magnetic field is created 'on the fly'. Opposite to this the small loop is a magnetic antenna, it creates a magnetic field 'on the spot' while the electric field is created 'on the fly'.
As a result of this the main source of losses for a short vertical monopole is in the environment (ground, trees, buildings etc.) while for a small loop the major losses are within the antenna. Therefore a small loop is less dependent on the environment for its functionality.
But for both types of antennas the goal is to get the ratio of radiation resistance versus loss resistances as large as possible. In practice most amateurs achieve better results with short vertical monopoles, only when environment losses are extremely high a small loop will be superior.
Remark : Throughout these pages the terms ERP, EIRP, dBi and dBd will be used frequently. If you are not familiar with these terms I would recommend to read this first.
2.1. Vertical monopole antenna
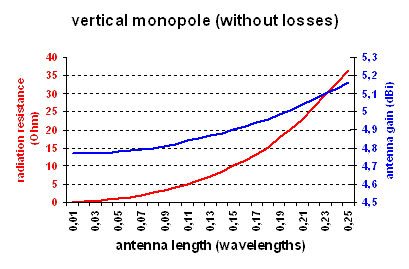
Most radioamateurs are familiar with the quarter-wave vertical monopole antenna, often also called a "Marconi antenna". It is a quarter wave long, is fed against ground (eventually improved by a radial system) and has a radiation resistance of 36 . The dimensions of a quarter wave vertical antenna might be suitable from the 40m band upward, some brave hams might even have this antenna for 80m and 160m. But for 136kHz it would be over 500m (1500ft) high, without doubt beyond the range of any ham. Thus at longwave there is no other way than using a vertical monopole that is (very) much shorter than a quarter wave.
. The dimensions of a quarter wave vertical antenna might be suitable from the 40m band upward, some brave hams might even have this antenna for 80m and 160m. But for 136kHz it would be over 500m (1500ft) high, without doubt beyond the range of any ham. Thus at longwave there is no other way than using a vertical monopole that is (very) much shorter than a quarter wave.
When a vertical monopole is less than a quarter wave (it's natural resonance) a few things change :
The effect of the antenna length on the radiation resistance and antenna gain can be seen on the first picture at the right. So, in contradiction to what many believe, the antenna gain of a short vertical monopole is only 0.4dB less that that of a fullsize quarter wave vertical (even if the short monolope is only a fraction of the wavelength). Nevertheless the performance of a short vertical monopole is -20dB to -40dB below that of a quarter wave vertical, because the efficiency (ratio of radiation restistance and loss resistances) rapidly decreases as the antenna becomes shorter.
Example :
1. A Quarter wave vertical has a radiation resistance of 36 and a loss resistance (groundloss) of 10
and a loss resistance (groundloss) of 10 . The efficiency of this antenna is :
. The efficiency of this antenna is :
 , while there is a groundloss of 50
, while there is a groundloss of 50 and a loss in the loading coil of 20
and a loss in the loading coil of 20 . The efficiency of this antenna is :
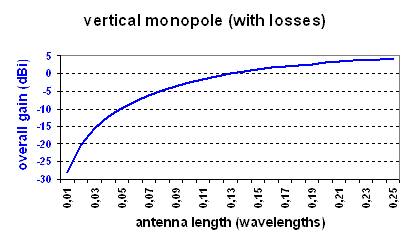
. The efficiency of this antenna is :The second picture shows "overall gain" (efficiency + antenna gain) of an average antenna as a function of its length.
2.2. Short vertical monopole
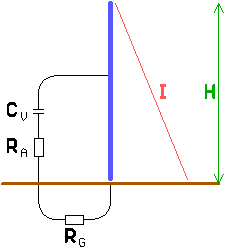
Assume we have a short vertical monopole with a height H and fed against ground. If H is small compared to the wavelength then :
The current distribution, that is different from the sinusoidal distribution we are used to, can be explained as follows :
The antenna capitance is not located at one single point on the antenna, but is distributed equally over the antenna. As the antenna current flows into the antenna it gradually 'disappears' via the distributed antenna capacitance, resulting in a linear decrease.
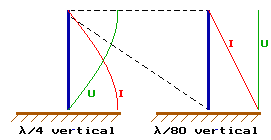
Another - and maybe more correct - way to look at it is to compare a short vertical with a full size (quarter wave) vertical. The full size vertical has a sinusoidal current and voltage distribution whith a 90 degrees phase shift between U and I. The short vertical can been seen as just the end of a fullsize vertical, where the voltage distribution is (almost) constant and the current distribution decreases (almost) linear.
The radiation resistance of a short vertical monopole with a height H and at a wavelength 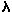 is :
is :
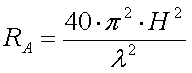 [1a]
[1a]
For 136kHz this becomes :
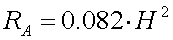 [1b] (RAin m
[1b] (RAin m and H in m)
and H in m)
The capacitance of a vertical wire of a height H and diameter d is :
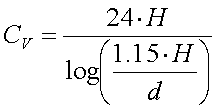 [2a] (CV in pF, H and d in m)
[2a] (CV in pF, H and d in m)
In most cases the simplified formula CV = 6pF/m [2b] is accurate enough.
In order to get a maximum radiated power we need a maximal current through the antenna. This can be done by compensating the capacitive component with an inductive component (loading coil), or otherwise said : bringing the antenna to resonance. Based on the formula for resonance (Thomson formula) we can calculate the inductance we need (see the chapter "Loading coil" for details).
Example :
Assume we have a 10m long vertical wire (3mm diameter) with and an enviromental loss of 60 .
.
Based on formula 1a the radiation resistance is calculated as 8.2m , the antenna capacitance, based on formula 2a is 67pF. To bring the antenna to resonace on 136kHz we will need a loading coil of 20.2mH. The reactance of the coil is 17.4k
, the antenna capacitance, based on formula 2a is 67pF. To bring the antenna to resonace on 136kHz we will need a loading coil of 20.2mH. The reactance of the coil is 17.4k , so if we assume a Q of 300 then the coil-loss will be 58
, so if we assume a Q of 300 then the coil-loss will be 58 . This brings the total loss resistance to 118
. This brings the total loss resistance to 118 .
.
If we put a power of 100W into the antenna we will have an antena current of 0.92A, resulting in 6.95mW radiated power and a voltage of 16kV over the loading coil.
In the above example we calculated a radiated power of 6.95mW (0.92A into 8.2m ). To get the ERP (Effective Radiated Power) we have to take the gain of the antenna into account, for a short vertical monopole this is 2.6dBd. So the calculated power in this case will be 12.6mW ERP.
). To get the ERP (Effective Radiated Power) we have to take the gain of the antenna into account, for a short vertical monopole this is 2.6dBd. So the calculated power in this case will be 12.6mW ERP.
2.3. Vertical antenna with capacitive toploading
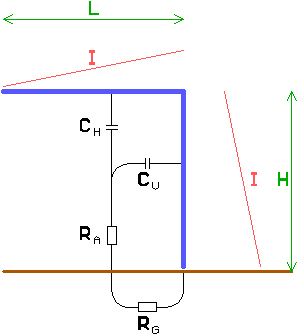
The efficiency of a short vertical antenna can be improved by increasing the radiation resistance. This is done my improving the current distribution over the antenna, as the radiation resistance is proportional to the square of the average current through the vertical section. For a short vertical monopole, as described above, the average current is 50% of the current at the feeding point. One way to improve the current distribution is to add capacitive toploading to the vertical antenna.
The current distribution over the antenna has still a linear decrease, but due to the fact that the minimum now is at the end of the horizontal section the average current in the vertical part is higher.
The capacitance of a horizontal wire with a length L, a diameter d and at a height H is given by :
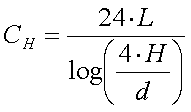 [3a] ( CH in pF, H, L and d in m)
[3a] ( CH in pF, H, L and d in m)
In most cases the simplified formula CH = 5pF/m [3b] is accurate enough.
The total antenna capacitance CA = CV + CH. The antenna current at the top of the vertical section is determined by the ratio of CH and CV (assuming that the same amount of current 'disappears' via every pF) :
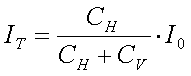 [4a]
[4a]
Thus the average current through the vertical section is :
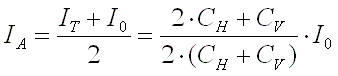 [4b]
[4b]
And the radiation resistance is proportional to the square of the average current through the vertical section, relative to the average current in a vertical monopole (IA = I0/2) :
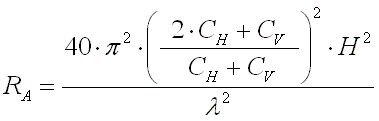 [5a]
[5a]
for 136kHz this is :
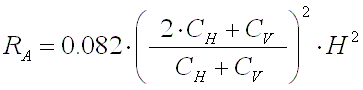 [5b] (RAin m
[5b] (RAin m and H in m)
and H in m)
This means that the radiation resistance can be quadrupled by adequate capacitive toploading.
An additional benefit of capacitive toploading is that the antenna capacitance can increase significantly. Therefore the inductance (loading coil) needed will decrease, resulting in lower losses in and lower voltages over the loading coil.
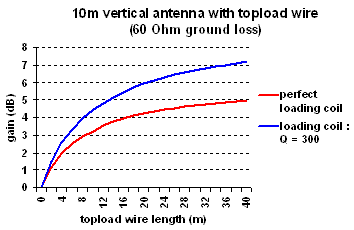
Example :
Assume we still have the 10m long vertical wire (3mm diameter) and the enviromental loss of 60 of the previous example, but now we extend the antenna with a 20m long horizontal topload wire (at 10m height).
of the previous example, but now we extend the antenna with a 20m long horizontal topload wire (at 10m height).
The capacitance of the vertical section will be 67pF (formula 2a) while the capacitance of the topload will be 116pF (formula 4a), resulting in a total antenna capacitance of 183pF. The radiation resistance will be 21.9m (formula 5a). The loading coil must be 7.4mH, at a Q of 300 the loss in the coil will be 21
(formula 5a). The loading coil must be 7.4mH, at a Q of 300 the loss in the coil will be 21 and the total loss will be 81
and the total loss will be 81 .
.
If we put a power of 100W into the antenna we will have an antenna current of 1.11A, resulting in 27mW radiated power and a voltage of 7kV over the loading coil. Taking into account the gain of 2.6dBd the ERP will be 49mW, this an overall 5.5dB improvement compared to the same antenna without capacitive topload.
The gain that can be achieved by having a better current distribution is 6dB, but due to the increased capacitance (and thus a smaller loading coil needed) some dB extra gain can be won, as you can see in the graph.
A vertical antenna with capacitive toploading can be constructed in various configurations, besides the 'inverted-L' configuration there are also the 'T' and 'umbrella' configurations that are frequently used. In general any shape of capcitive topload will work, the goal should be to get an many wire as possible as high in the air as possible. The topload wires can be sloping (umbrella antenna), but this will cause a decrease in the radiation resistance. As a rule of thumb can be said that sloping topload wires should never come lower than 50% of the antenna height.
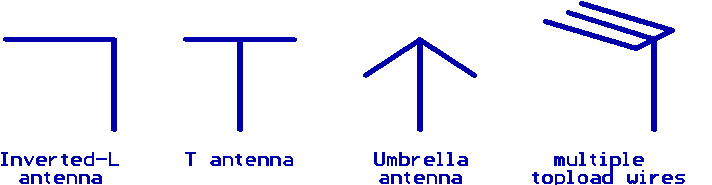
The amount of topload capacitance is often limited by the space available. To get maximal topload capacitance on a limited space parallel wires can be used. Practical results proved that capacitances upto 15pF/m can be achieved, while a single wire is about 5pF/m :
| Station | number of wires | Spacing | Height above ground | Capacitance |
| EI0CF | 4 | *1m*4m*1m* (1) | 10m | 15pF/m |
| G3XDV | 3 | all 0.5m - 1m (2) | 14m | |
| G3AQC | 3 | all 0. 45m | 13.5m | 12pF/m |
| ON7YD | 4 | all 0.8m | 12.5m | 13pF/m |
2.4. Umbrella antenna
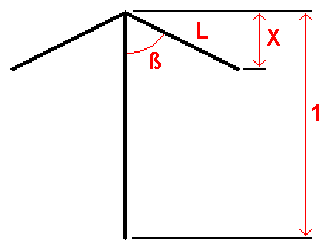
For practical reasons many toploaded verticals have sloping topload wires. These kind of antennas are called umbrella antennas. A sloping topload wire has 2 contradictory effects on the radiation resistance (RA) of the antenna. One the one hand it increases the top capacitance, thus increasing RA. But on the other hand it will introduce a 'downward current' that cancels a part of the (upward) current through the vertical, thus decreasing RA.
The influence of both effects depends of the number of topload wires, their length and their sloping angle. John Sexton (G4CNN) did develop a mathematical model for umbrella antennas with the goal to optimize the parameters (number of wires, length and sloping angle) for a maximum radiation resistance.
Detailed calculations how to optimize the slope and length of the topload wires can be found here.
Assume an umbrella antenna with a unity height (1) and n topload wires of a length L, sloping under an angle ß. The topload wires will 'shield' the vertical part over a length X = L*cos(ß).
The gain (in dB, relative to a vertical without toploading) will be :
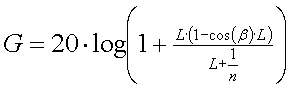 [6] (log = 10 based logaritm, L and X relative to the unity height '1')
[6] (log = 10 based logaritm, L and X relative to the unity height '1')
The graphs below give the relative gain of an umbrella antenna for sloping angles of 30, 45 and 60 degrees - depending on the 'shielding length' (X) and the number of tophat wires :
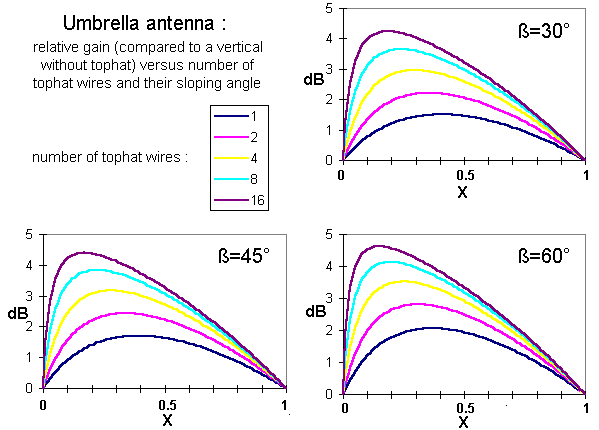
As expected higher sloping angles give the better results, but also note that for a certain sloping angle many short tophat wires are more effective than a few long.
The above formula and graphs assume that the tophat wires do not affect each other. In practice this will not be true in the case of many short tophat wires, the effective gain will be less than the calculated one.
2.5. Capacitive toploading of single-tower antennas
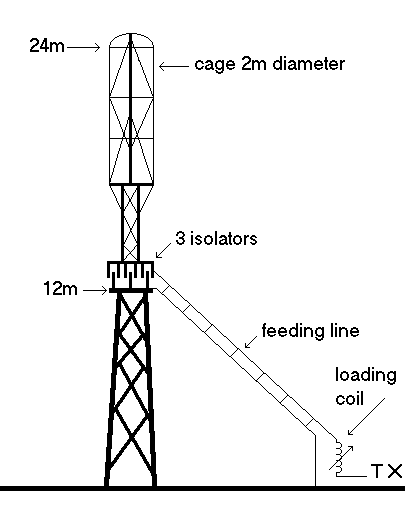

In the previous chapter (umbrella antennas) an example was given how a capacitive toploaded antenna can be built using a single support tower. If the space to put up the antenna is even more limited there are some alternative ways to provide your antenna of an efficient capacitive toploading. The above pictures show one way to achieve this, as done by Werner De Bondt (ON6ND). At the top of a grounded 12m tower there is a large isolated cage that provides a high capacitance toploading. Additional experiments done by ON6ND have shown that the antenna efficieny can be further improved by placing (a part of) the toploading at the bottom of the isolated section. Werner noticed a 1 S-point (6dB) improvement by doing so. Further there was no difference noticed when the feeding line was replaced by a single wire.
2.6. Spiral toploaded antenna
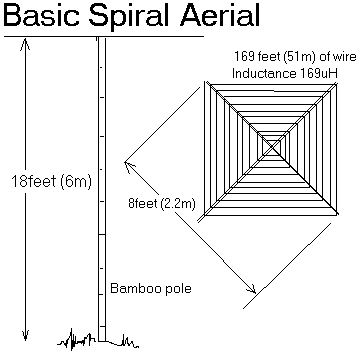
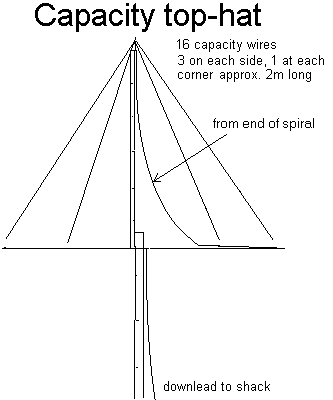
Alan Melia (G3NYK) and Finbar O'Connor (EI0CF) developed an efficient LF antenna on a limited space. The topload of the antenna has both an inductive as capacitive component. The spiral part works both inductive as capacitive while the piramidal tp hat provides additional capacitive toploading. Despite the limited dimensions the antenna could be brought to resonance on 136kHz with a relative small (2mH) loading coil.
A complete description of this antenna can be found on G3NYK's webpage.
2.7. Vertical antenna with inductive toploading
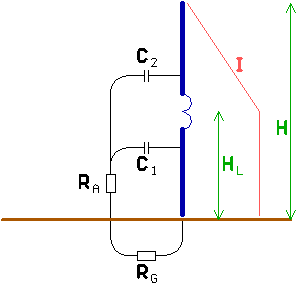
Another way to improve the current distribution over the antenna is to place to loading coil at an elevated point (HL) of the antenna.
As the voltage is built up over the loading coil, only the part of the antenna above the coil wil be at high voltage. The voltage at the lower part of the antenna is negligible so the antenna current will not 'disappear' via the capacitance C1, only via C2. The antenna current below the loading coil will remain at maximum value and the result is an improved average current :
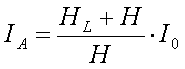 [7]
[7]
The radiation resistance of a vertical antenna with elevated loading coil is :
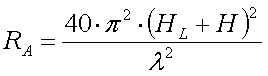 [8a]
[8a]
For 136kHz it is :
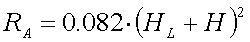 [8b] (RA in m
[8b] (RA in m )
)
Example :
Assume we have a 10m high vertical wire (3mm diameter) and 60 enviromental loss. If we place an elevated loading coil at 5m height the radiation resistance will increase from 8.2m
enviromental loss. If we place an elevated loading coil at 5m height the radiation resistance will increase from 8.2m to 18.5m
to 18.5m (resulting in a theoretical gain of 3.5dB). But at 5m height we will need a loading coil of 40.4mH, at a Q = 300 the coil-loss will be 116
(resulting in a theoretical gain of 3.5dB). But at 5m height we will need a loading coil of 40.4mH, at a Q = 300 the coil-loss will be 116 . This brings the total loss to 176
. This brings the total loss to 176 .
.
If we put a power of 100W into the antenna we will have an antenna current of 0.75A, resulting in 10.5mW radiated power and a voltage of 26kV over the loading coil. Taking into account the gain of 2.6dBd the ERP will be 19.1mW, this only a 1.4dB improvement compared to the same antenna without elevated loading coil.
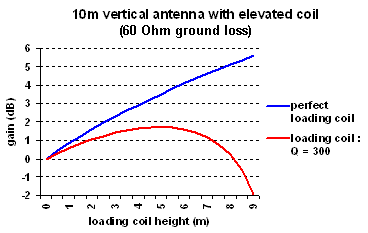
As shown in the example, inductive toploading has also a disadvantage :
The loading coil has to be resonant to the antenna capacitance of the upper part (C2) what means that the inductance has to be larger as the coil is placed higher. A larger coil means also a larger coil-loss and from a certain height the additional loss induced by the larger coil cannot be compensated by the improved current distribution, as you can see in the graph at the right. Apart from that the voltage over the loading coil increases and stable mounting of an elevated loading coil creates also mechanical problems.
2.8. Vertical antenna with capacitive and inductive toploading
The radiation resistance of a short vertical monopole with limited capacitive toploading can be improved significantly by adding inductive toploading (elevated loading coil).
But based on the improvement of the current distribution, adding inductive toploading to an antenna with sufficient capacitive toploading is not very efficient. In most cases the theoretical gain is no more than 0.1 or 0.2dB. Practical experiments by a number of amateurs however have shown that in some cases combined capacitive / inductive toploading can lead to a significant gain (of up to 5dB).
More detailed information about combined capacitive / inductive toploading can be found here.
2.9. Vertical antenna with tuned counterpoise
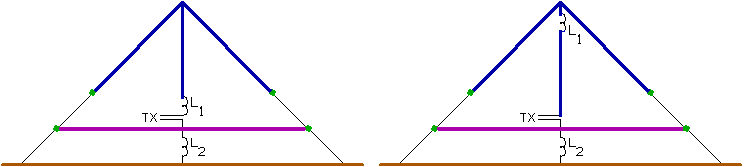
Pat Hawker describes in an article in ELECTRONICS WORLD + WIRELESS WORLD (February 1990) a kind of umbrella antenna with a tuned counterpoise. Both the antenna and the counterpoise are isolated from the ground.
The antenna is tuned by the loading coil (L1), an elevated loading coil can be used to improve the current distribution. By adjusting L2 the counterpoise is tuned to minimize ground loss. In practice L2 has to be tuned for maximal signalstrength in the far field.
This type of antenna has been used successfully on mediumwave with a gain upto 5dB measured by adding the tuned counterpoise. To my knowledge this antenna has not been tested by amateurs on 136kHz, but it might be worth a try.
No references to calculate the value of L2 are given, but the article refers to US Patent no 3,742,511 and to IEEE Trans. on Broadcasting, June 1989, pages 237-240
(download it as zipped GIF file).
2.10. Meander antenna
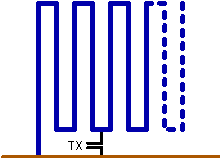
The performance of meander antennas for shortwave is described by Warnagiris and Minardo in IEEE Trans. on Antennas and Propagation, December 1998, pages 1797-1801. They show that the radiation resistance of short electrical antennas, such as a short vertical monopole, can be significantly increased by using u number of folded elements. Experimental investigations on a 44cm high meander antenna with 21 elements resulted in a resonance on 20.1MHz and an impedance of 21.9 . For a simple vertical monopole of the same length a radiation resistance of 0.34
. For a simple vertical monopole of the same length a radiation resistance of 0.34 can be expected. When scaled to 136kHz this 0.029 wavelength antenna becomes 64m high and for the 21 elements over 1.3km (!) of wire would be needed. But, assuming 60
can be expected. When scaled to 136kHz this 0.029 wavelength antenna becomes 64m high and for the 21 elements over 1.3km (!) of wire would be needed. But, assuming 60 groundloss, this antenna would perform almost 18dB better than a vertical monopole of the same height.
groundloss, this antenna would perform almost 18dB better than a vertical monopole of the same height.
A meander antenna can be built rather compact arround a grounded tower.
The line-spacing has to be at least 20 times the wire diameter for optimal performance. Further experiments have shown following Size Reduction Factor (SRF) versus the number of lines (N) :
| SRF | N | antenna height | wirelength |
| 0.6 | 3 | 329m | 987m |
| 0.3 | 9 | 164m | 1481m |
| 0.15 | 27 | 82m | 2221m |
| 0.075 | 81 | 41m | 3332m |
| 0.0375 | 243 | 20.5m | 4998m |
| 0.01875 | 729 | 10.3m | 7497m |
For acceptable antenna heights (20m and less) the number of elements and the wirelength needed are not very realistic. Using 3mm Cu-wire (loss = 1 per 100m at 136kHz) the 20m version would have a 50
per 100m at 136kHz) the 20m version would have a 50 wire-loss, the 10m version even 75
wire-loss, the 10m version even 75 . The weight of the wire would be resp. 330kg and almost 500kg.
. The weight of the wire would be resp. 330kg and almost 500kg.
But a meander antenna with a limited number of elements and tuned to resonance by a loading coil could be an acceptable alternative antenna for 136kHz. But remember that a meander antenna has many resonances at higher frequencies, so an adequate filtering of the transmitter signal (harmonics !) will be necessary.
To my knowledge meander antennas have not been used by amateurs on longwave so far.
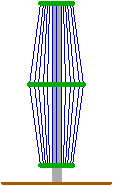
2.11. Antenna with multiple vertical elements
The radiation resistance of a short vertical monopole can be significantly improved by the use of multiple vertical elements. These elements are connected through the capacitive topload wires and the antenna is fed through one of the elements, while the others are connected to ground. The radiation resistance will increase with the square of the number of elements, x4 for 2 elements, x9 for 3 elements etc...
If each of the elements has its own ground-network this can reduce the total loss-resistance.
But this system has also a disadvantage : as all the elements share the same capacitive topload the capacitance of each individual element will decrease and larger loading coils will be needed, resulting in additional coil-losses and a higher antenna voltage.
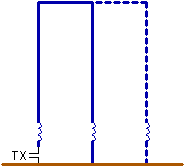
2.12. Using a non isolated antenna tower as LF-antenna
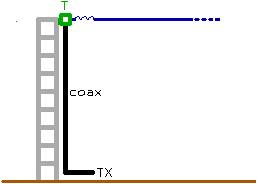
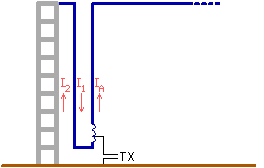
A short vertical monopole normally has to be isolated from ground at its base. But most antenna-towers are not isolated, for mechanical and electrical safety reasons. Here are 2 possibilities shown how to use a non isolated tower as vertical antenna for longwave :
2.13. Antennas with a long horizontal section
Based on the calculated current distribution and coil-losses very little gain can be won by having a horizontal section that exceeds the length of the vertical section by more than a factor 5. The only advantage would be a decraase of the groundloss due to the larger 'footprint' of the antenna (see 3.6.3).
But in practice several hams achieved very good results using antennas with a very long horizontal section and it is difficult to explain this results just by the lower groundloss. OH1TN uses an antenna with a horizontal section of about 500m, bringing the antenna to resonance on 136kHz without inductive loading (sse picture below).
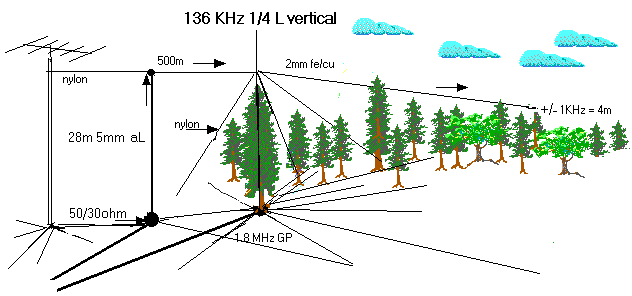
Despite the fact that the antenna is mainly horizontal, its polarization is mainly vertical as long as the height of the antenna (compared to the wavelength) is low and it is a monopole antenna (with ground as counterpart). An example of a large horizontal antenna with vertical polarization is the DDRR antenna.
2.14. Helical antenna
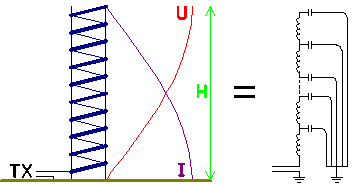
In the helical antenna the loading coil (or a part of it) is incorporated in the vertical section of the antenna. So with this antenna both capacitance and inductance are distributed over the entire antenna. As the antenna voltage builts up over the loading coil, the antenna voltage increases with the height. This voltage increase results in an improved current distribution, as in the lower part of the antenna (where the voltage is low) less current will 'disappear'. Without capacitive toploading the radiation resistance of a helical antenna will be 1.54 times larger as for a 'straight' vertical of the same height, this is a gain of 1.9dB.
When capacitive toploading is added the advantage of a helical antenna will be less, for 2 reasons :
An additional problem is that it is not so easy to built a mechanical stable helical antenna . The only amateur who - to my knowledge - used a helical antenna with succes was Toni Baertschi (HB9ASB), until the antenna was destroyed in a storm (december 1999).
2.15. Short vertical dipole
So far I am not aware of any short vertical dipole used by hams or lowfers on LF, but it could be an alternative for the short vertical monopole.
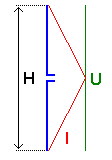
* Short dipole in free space
The radiation resistance of a short dipole with a length H and at a wavelength 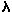 , in free space, is :
, in free space, is :
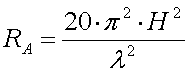 [9a]
[9a]
For 136kHz it becomes :
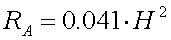 [9b] (RA in m
[9b] (RA in m and H in m)
and H in m)
The antenna gain of a short dipole in free space is 1.76dBi
* Short vertical dipole close to ground
Antenna simulation shows that close to ground the radiation resistance of a short vertical dipole doubles (versus the free space value) and that the antenna gain increases to 4.77dBi. This means that both radiation resistance and antenna gain would be identical to these of a short vertical monopole of the same size. But at the same time it can be expected that the enviromental losses will increase, due to the high antenna voltages close to ground.
Jim Moritz (M0BMU) comments a short vertical dipole close to ground as follows :
A short vertical dipole in free space would have a symmetrical current distribution, maximum in the middle and zero at the ends. Placing it close to a ground plane would modify this because displacement current would flow between the ground plane and the lower half of the dipole, increasing the current towards the bottom end of the dipole making the current distribution more even in the lower part of the dipole. The current distribution in the case where the lower end of the dipole was very close to the ground would be very similar to that of a short monopole with an elevated feed point - if the lower end of the dipole actually was in contact with the ground plane, it would be a monopole of course.
You could increase the capacitance by adding end loading to the dipole - if the lower end of the dipole were close to the ground, in effect you would have a top-loaded vertical with an elevated feed driven against a counterpoise.
A practical difficulty would be caused by the asymmetrical nature of the dipole - it would be necessary to have some way of adjusting the voltages applied to the upper and lower legs of the dipole to get equal current in both legs, and zero net current on the feed line, in order to achieve the proper dipole operation. Since the lower end of the dipole would be a high voltage point, and close to the ground, there would be increased dielectric losses in the ground under the antenna, which would tend to reduce any advantage of this antenna configuration.
2.16. Why a horizontal dipole is a rather inefficient antenna on LF
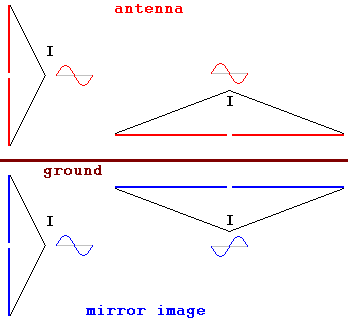
As in most cases height is the limiting factor to built large (and efficient) LF antennas it is tempting to built a large horizontal antenna. Although antennas with a large horizontal section have proved to be quite usefull on LF (see " Antennas with a long horizontal section ") a horizontal dipole is a rather inefficient antenna on LF.
If an antenna is placed above (a perfect) ground a "mirror image" is created with the ground as mirror plane. For a vertical antenna this causes no problem as both the real antenna and its mirror image are in phase. But for a horizontal antenna the mirror image is in counterphase, so if the antenna is close to ground the mirror image will cancel out most of the signal (see picture at the right).
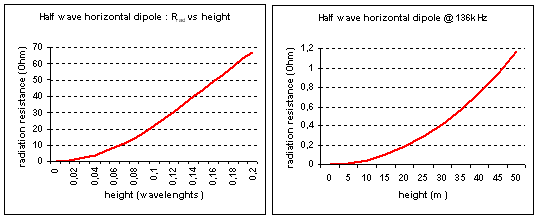
In practice this results in a decreasing radiation resistance as the antenna comes closer to ground. At very low heights (in wavelengths !) even the radiation resistance of a full size half wave dipole is only a fraction of an  . On 136kHz any amateur sized antenna is at low height above ground and one would need a full size dipole at at least 50m height to achieve a radiation resistance of 1
. On 136kHz any amateur sized antenna is at low height above ground and one would need a full size dipole at at least 50m height to achieve a radiation resistance of 1 . (see graphs below).
. (see graphs below).
2.17. Safety precautions
Be aware that - apart from the typical safety precautions one should always take in regard with the mechanical stability of antennas - there is a possible hazard that is typical for short vertical antennas : high voltages.
As mentioned before most short vertical antennas need a rather large loading coil to be brought to resonance. The voltage built up over this coil can be some tens kV, in combination with a moderate to high power TX this voltage (or better said : the current caused by this voltage) can be harmfull or even lethal.
Example :
Assume a 10m high vertical antenna with a capacitance of 70pF. This antenna will need a 19mH loading coil, that has a reactance of over 16k . Further assume a loss resistance of 80
. Further assume a loss resistance of 80 (40
(40 loss in the loading coil + 40
loss in the loading coil + 40 ground loss) and a TX power of 400W, this will cause an antenna voltage of 36kV and an antenna current of 2.2A.
ground loss) and a TX power of 400W, this will cause an antenna voltage of 36kV and an antenna current of 2.2A.
Fortunately voltage and current are almost 90 degrees phase shifted and touching a high voltage part of the antenna will cause a breakdown of the antenna voltage, but it can still cause serious burnings or worse.
An interesting fact is that a larger antenna (that has a larger capacitance and thus requires a smaller loading coil) will have a lower antenna voltage. A small backyard antenna can be a much higher potentional danger than a monster antenna.
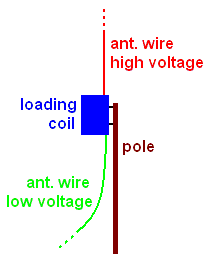
In any case one should take the nessecary precautions to avoid that high voltage parts of the antenna can be touched. Since the voltage builts up over the loading coil, placing this coil at a certain hight can be a simple and effective solution. But keep in mind that even at the low voltage side (before the loading coil) the voltage can be up to a few 100V, so even there one should only use sufficient isolated wire.

Another effect of the high antenna voltage can be the corona effect. This is an electric discharge resulting from the ionization of the air and occurs mainly at sharp ends and edges of the antenna. The corona effect should be avoided as it is a loss of power and, even worse, the arcing eventualy can start a fire.
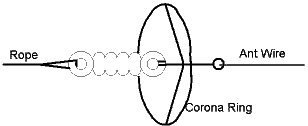
The corona effect is rather seldom reported by amateurs on LF, from the information I received the antenna voltage was in excess of 30kV in all cases. The corona effect can be surpressed by avoiding any sharp ends or edges and mounting corona rings at the ends of the antenna.
2.18 Bringing a short vertical monopole to resonance
2.18.1. Loading coil
If you will connect you TX directly to a short vertical monopole you will hardly transmit any signal (and get a vey bad SWR), This is due to the mainly capacitive impedance of several 1000  . To bring a short vertical monopole to resonance this capactive component has to be compensated by the inductance of the loading coil.
. To bring a short vertical monopole to resonance this capactive component has to be compensated by the inductance of the loading coil.
The inductance L (in Henry) can be calculated using the Thomson formula :
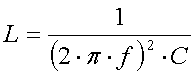 [10a] (f = frequency in Hz and C = antenna capacitance in F)
[10a] (f = frequency in Hz and C = antenna capacitance in F)
For 136kHz it is :
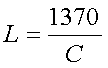 [10b] (L in mH and C in pF)
[10b] (L in mH and C in pF)
Example :
If we want to bring an antenna with a capacitance of 300pF to resonance at 137kHz then we will need a loading coil of 4.5mH.
The inductance L (in µH) of a single layer coil is :
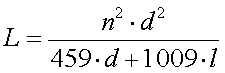 [11]
[11]
(n = number of turns, d = coil diameter in mm and l = coil length in mm)
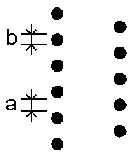
For the typical sizes of LF loading coils formula 11 will give the inductance within a few %, but in fact the inductance will also be dependent of the wire diameter (b) and wire spacing (a).
Formula 11 is valid for wire spacing = wire diameter. If this is not the case you will have to add a 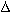 L to the inductance calculated with formula 11 :
L to the inductance calculated with formula 11 :
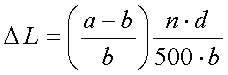 [12]
[12]
(a = wire spacing in mm, b = wire diameter in mm, n = number of turns and d = coil diameter in mm)
Be aware that 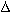 L can be negative (if a < b), thus the inductance will be less that the one calculated with formula 11.
L can be negative (if a < b), thus the inductance will be less that the one calculated with formula 11.
Not only the inductance but also the Q-factor of the coil will be affected by the ratio of wire diameter and wire spacing. This is due to losses caused by the proximity effect. Experiments have shown that best Q is achieved when the wire diameter and the wire spacing are equal (a = b). Small (or no) wire spacing will result in a relative small coil (least wire needed), but with a realtive low Q. If the wire spacing is very large then there will be little losses caused by the proximity effect but you will need much more wire to achieve a certain inductance causing more additional loss than you gained from eliminating the proximity effect.
Example :
Assume we have a coil made of 100 turns of 2mm diameter wire with 2mm spacing. The coil diameter is 300mm.
100 turns of 2mm wire with 2mm spacing make a 400mm long coil. Using formula 11 the inductance is 1.66mH. If we leave the coil length and diameter unchanged but use 1mm diameter wire (and 3mm spacing) then the inductance will increase by 0.12mH (formula 12) and will be 1.78mH. If instead 3mm wire (and 1mm spacing) is used, the inductance will decrease by 0.01mH and will be 1.65mH.
2.18.2. Coil losses : the Q-factor
As any other coil the loading coil will also have certain losses that will reduce the overall efficiency of the antenna system.
The Q-factor is the ratio of the inductive reactance (XL) and the loss resistance (R) :
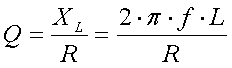 [13] (XL and R in
[13] (XL and R in  , f = frequency in Hz and L = coil inductance in H)
, f = frequency in Hz and L = coil inductance in H)
Example :
A 3mH coil with a loss resistance of 8 will have a Q of 320 at 136kHz
will have a Q of 320 at 136kHz
The loss resistance of the coil is caused by :
On LF in most cases these last losses can be ignored if some care is taken by selecting the form material and the location of the loading coil. The Ohmic losses are determined by the resistance of the coil. Due to 2 effects the restistance of the coil will be frequency dependent and often will be considerably larger than the DC resistance :
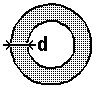
a. Skin effect
As the frequency get higher the current through a wire will tend to flow mainly throught the outer layer, with little or no current through the centre of the wire. Since only a part of the wire surface is used the AC resistance will be larger than the DC resistance and will increase as the frequency increases.
The thickness of this outer layer (d) is :
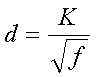 [14] (d = skin layer in mm, K = material dependent constant and f = frequency in kHz)
[14] (d = skin layer in mm, K = material dependent constant and f = frequency in kHz)
| Copper | Aluminium | Messing | Silver | Gold | |
|---|---|---|---|---|---|
| K | 2.08 | 2.77 | 4.45 | 2.02 | 2.37 |
| conductivity (S/m) | 58x106 | 33x106 | 13x106 | 62x106 | 45x106 |
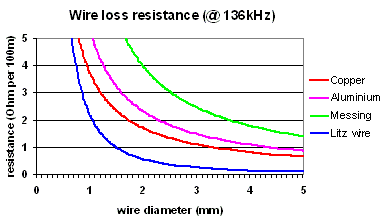
This means that for 136kHz the skin layer is 0.18mm for copper and 0.24mm for aluminium. Although messing has a thick skin layer (0.38mm at 136kHz) it not suitable due to its poor conductivity. The most economic solution is the use of copper wire, but at a wire diameter of 3mm and above aluminium is only slightly worse and can give you a considerable lighter coil (it has only 30% of the weight of copper).
Once the wire diameter exceeds twice the skin depht the wire has 'wasted space' inside. Thus it is more efficient to use 2 (or more) thin wires in parallel than a single thick wire. Such HF-wire consisting a large number of parallel (isolated) wires is called litz wire. It is a very good choise to built a coil as a litz wire will only have a fraction of the loss of a single wire of the same diameter, but unfortunately it is also rather expensive.
Be aware that in multi-stranded wire the individual parallel wires are not isolated, so this is not litz wire !
b. Proximity effect
When an AC current is flowing through 2 wires that are close together the currents will tend to flow at maximum distance from each other, causing an effect similar to the skin effect. This will cause an additional increase of the loss resistance. This effect can be minimized by inceasing the wire spacing. But as the wire spacing is increased one will need mure turns (and thus more wire) to achieve the same inductance. So what is won by reducing the proximity effect is lost again (or even worse). Experiments have shown that the lowest loss is achieved when the wire spacing equals the wire diameter.
Special coil winding techniques have been developed to keep the turns of a coil as far as possible apart without increasing the coil dimension (and thus needing more wire). One of these techniques is basket weaving where the coil former is made of an odd number of rods and the wire is 'weaved' between them. That way high-Q coils can be made, even 'flat' coils and variometers, as shown below.
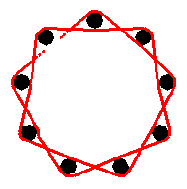


Remark : the proximity effect as shown here will happen if the currents flow in the same direction, as always will be the case in a coil. If the currents are flowing in opposite directions the proximity effect will be similar, except that the currents now will tend to flow close to each other.
c. Optimizing coil dimensions
Apart from the wire material and diameter also the ratio of coil diameter / coil height and the ratio of wire spacing / wire diameter will affect the Q-factor. Best Q-factor can be expected for a coil diameter / coil height ratio of ± 1.4 and a wire spacing / wire diameter ratio of ± 1.
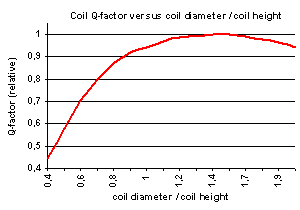
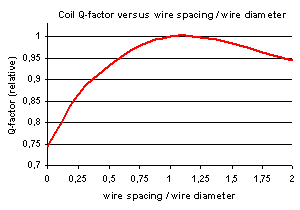
The dimensions of an optimized coil (coil diameter / coil height = 1.4 and wire spacing / wire diameter = 1) are :
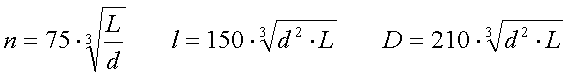 [15]
[15]
(n = number of turns, L = inductance in mH, d = wire diameter in mm, D = coil diameter in mm and l = coil length in mm)
Example :
Assume we want to make a 2mH coil optimized for best Q-factor, using 3mm diameter wire. Based on formula 15 we will need 66 turns on a coil of 39.3cm long and a diameter of 55cm.
d. Pyramid wound coils (by Niels Jorgensen, OZ8NJ)
A special technique called "Bank" or "Pyramid" winding to contruct compact and high-Q loading coils for 136kHz. This method was used to build coils and variometers for LF / MF marine and aero transmitters.
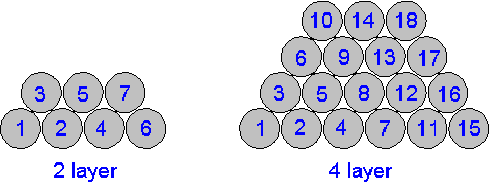
The advantages of the method are obvious :
The drawback is that the proximity losses will increase, but the overall effect is positive.
Although 4 and 5 layer coils of this type do exist practical difficulties to keep the windings in place will often limit Pyramid winding to 2 layers.
2.18.3. Variometer

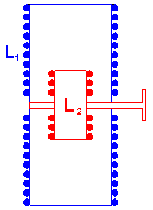 In practice the loading coil will have to be adjustable in order to correct for the day-to-day variations of the antenna capacitance (due to changing weather conditions). These variations are rather small and can be corrected by minor variation of the loading coil (few %). But in many cases amateurs will experiment with different types of antennas and therefore will need a loading coil that can be adjusted over a larger range such as from 2 to 5mH (250% !).
In practice the loading coil will have to be adjustable in order to correct for the day-to-day variations of the antenna capacitance (due to changing weather conditions). These variations are rather small and can be corrected by minor variation of the loading coil (few %). But in many cases amateurs will experiment with different types of antennas and therefore will need a loading coil that can be adjusted over a larger range such as from 2 to 5mH (250% !).
For relative small variation of the loading coil inductance (up to 50%) a variometer can be used. This is a combination of 2 coils put in series, where a smaller coil (L2) is rotating inside the larger coil (L2). This way the inductance can vary from about L1-L2 to L1+L2. In theory a variometer could vary from 0 to 2*L (for L1 = L2 = L). But L2 has to rotate inside L1 and thus has to be smaller. Further will a too large L2 have a negative effect on the Q-factor of the variometer. As a result the practical limitation of the variometer range is 50%.
Instead of a small coil rotating inside a larger coil one can also use a small coil sliding in/out of a larger coil. But this design is not so popular as the mechanical construction is almost as complicated for a rotating variometer while variation of L is only half and the Q-factor varies strongly with the position of the sliding coil.

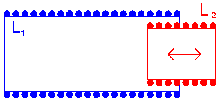 A high-Q variometer can also be built using 2 flat basket weaved coils, as shown here.
A high-Q variometer can also be built using 2 flat basket weaved coils, as shown here.
An alternative way to built a variometer is by sliding a ferrite rod in a coil. Care has to be taken that the rod material is not saturated and that the rod is not heating too much. If a small rod of the right material is used inide a large coil a variation up to 20% can be achieved without saturation or heating of the rod, even at a TX power of several 100W.
2.18.4. Tapped coil
For larger variations of L a tapped loading coil has to be used. Taps at different turns of the coil allow variation of L of several 100%, but these variation will be in steps. Therefore the combination of a tapped coil and a variometer is often used, either as a large tapped coil in series with a small variometer or as a 'all-in-one' solution where the large coil of the variometer is tapped.
2.18.5. Impedance matching
Bringing a short vertical monopole to resonance will ensure that any reactive component in the antenna impedance is compensated. Depending on the enviromental losses and loss in the loading coil the impedance will be in the range of 20 to 200 . This impedance has to be matched to the tramsmitter impedance, in most cases 50
. This impedance has to be matched to the tramsmitter impedance, in most cases 50 .
.
Although in may cases the antenna impedance will be in the range of 30 to 70 and thus the SWR without matching would be acceptable at first sight (less than 2:1) it might still be worth to match the antenna since :
and thus the SWR without matching would be acceptable at first sight (less than 2:1) it might still be worth to match the antenna since :
As matching an LF antenna is not much different from matching any other antenna just a brief overview of some matching techniques is given, with LF specific remarks.
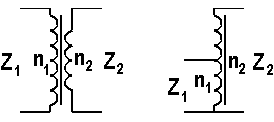
Transformer
Impedance matching can be done using a transformer, either a isolating or a non-isolating one (auto-transformer) :
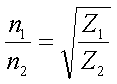 [16] (Z1 ... Z2 = impedances , n1 ... n2 = turns)
[16] (Z1 ... Z2 = impedances , n1 ... n2 = turns)
Example :
We want to match a 80 antenna to our 50
antenna to our 50 transmitter. That means that the ratio of the turns has to be 1.265. With n1 = 19 and n2 = 15 we come close to this value.
transmitter. That means that the ratio of the turns has to be 1.265. With n1 = 19 and n2 = 15 we come close to this value.
To allow matching to different impedances one (or both) sides of the transformer can be tapped. In most cases a toroid core will be used, although a ferrite rod might be used to. Care has te be taken in the choice of the core material, most materials that do fine on HF will either have too much loss or will require too much turns to be suitable on LF. Most manufacurers produce core material that is suitable for LF, but this can be rather hard to find. A low cost solution is to recuperate the "double-U" core that can be found in the HV-section of a TV set or monitor. Most of these cores can be used in low and medium power applications on LF (up to few 100W), but it is recommended to do regular checks on efficiency and overheating in the beginning.
The number of turns should be large enough, the inductance of the coils should be at least twice (and preferable 5 times) the impedances that have to be matched.
One of the advantages of a transformer is that it will work rather wideband and that it will still work stable at high tranformation ratios. Further the transformer provides a DC shortcircuit to ground and will ensure that there is no static charging on the antenna. In addition a transformer (not auto-transformer) provides a galvanic separation between the TX (RX) and antenna.
For more details on the designing of toroidal core transformers and an overview of suitable materials see here.
L-C network
 A simple L-C network can be used for impedance transformation :
A simple L-C network can be used for impedance transformation :
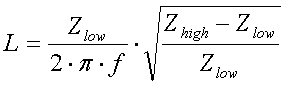 [17a]
[17a]
and
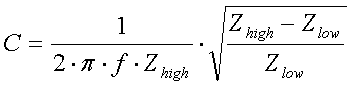 [17b]
[17b]
(L = inductance in H, C = capacitance in F, Zhigh ... Zlow = impedances in  and f = frequency in Hz)
and f = frequency in Hz)
For a frequency of 136kHz L and C can be calculated as :
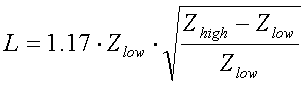 [17c]
[17c]
and
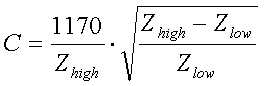 [17d]
[17d]
(L = inductance in µH, C = capacitance in nF and Zhigh ... Zlow = impedances in  )
)
Example :
We want to match a 80 antenna to our 50
antenna to our 50 transmitter. Based on formula 17 we will need a coil of 45.3µH and a capacitor of 11.3nF.
transmitter. Based on formula 17 we will need a coil of 45.3µH and a capacitor of 11.3nF.
Be aware that - in contradiction to a transformer - a L-C network is not widebanded. As the impedance transformation ratio increases the bandwidth will decrease. In order to have a stable network at 136kHz (ie. bandwidth of at least 2.1kHz) the transformation ratio should not exceed 5. For matching to 50 this will not be a problem (the antenna impedance can be in the range of 10 to 250
this will not be a problem (the antenna impedance can be in the range of 10 to 250 ). But one should take care if using a low impedance TX, in that case a cascade of 2 L-C networks should be prefered.
). But one should take care if using a low impedance TX, in that case a cascade of 2 L-C networks should be prefered.
Further one should choose the right capacitors. Most ceramic and metalfilm capacitors will have too much loss on LF. Capacitors that can be used are :
Be aware that - using high power - voltages up to several 100V can come across the capacitors, if you cannot find the high voltage types you can aventually use lower voltage types in series.
The inductances you will need are probably in the range of 20-200µH. At these values it is still possible to use air-coils, although they might be a bit bulky. If you use toroid cores ensure that the material is suitable for high-power and high-Q operation at LF, a lot of cores that do fine in (wideband) transformers will not perform well in L-C networks.
A L-C network will not provide a DC path to ground. So if you are using this kind of impedance matching it is recommended to provide an additional discharge path to ground (eg. a 10k / 5W resistor from the antenna side of the network to ground).
/ 5W resistor from the antenna side of the network to ground).
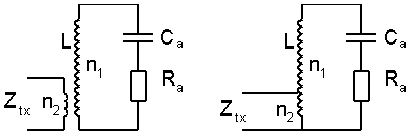
Resonance transformation
The impedance matching can also be done at the loading coil. Therefore you will need a second winding or a tap at the cold end of the loading coil.
Since for a short vertical monopole the reactive (capacitive) part of the antenna impedance is much larger than the resistive part (XCa >> Ra), the ratio of the turns is given by :
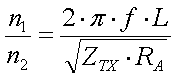 [18]
[18]
(L = loading coil inductance in H, f = frequency in Hz, n1 ... n1 = turns RA = antenna resistance in  and ZTX = transmitter impedance in
and ZTX = transmitter impedance in  )
)
The above formula assumes perfect coupling between the coil windings. For most loading coils this is not the case, so the exact ratio of n1/n2 will have to be determided by experiment. But the formula will still give a good value to start with.
Example :
We have an antenna with a (loss) resistance of 80 that is brought to resonance at 137kHz by a 3mH loading coil (200 turns). In order to match it to our 50
that is brought to resonance at 137kHz by a 3mH loading coil (200 turns). In order to match it to our 50 transmitter we will need a ratio of turns of 40.83 (formula 18). Since the loading has 200 turn we will need a secondary winding with 5 turns or tap the loading coil at 5 windings from the cold end.
transmitter we will need a ratio of turns of 40.83 (formula 18). Since the loading has 200 turn we will need a secondary winding with 5 turns or tap the loading coil at 5 windings from the cold end.
The advantage of resonance transformation is that it provides an all-in-one solution for matching and bringing the antenna to resonance. But at the same time this is also a disadvantage as changing the resonance will also affect the impedance matching and vice versa. With the practical values for antenna resistance and capacitance the ratio of turns will be rather large (50-200) and thus the impedance matching can be rather critical.
If you use a secondary winding this should always be placed at the cold (grounded) end of the loading coil, in order to avoid flash over (and all the destructive consequences) between the loading coil and the secondary winding.
2.18.6. Bandwidth considerations
The 136kHz ham band is only 2.1kHz wide (135.7-137.8kHz), so at first sight one would not expect bandwidth problems with the antenna. But keep in mind that 2.1kHz is 1.5% of 136kHz, so the relative bandwidth is about the same as the (European) 7MHz band and even more than the (European) 144MHz band. In addition antennas are very short, what decreases their bandwidth. So in some cases it can be required to retune the antenna when changing frequency.
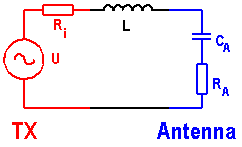
A short vertical monopole can be seen as capacitance (CA) in series with a resistance (RA). To bring the antenna to resonance a loading coil (L) is needed and the antenna is fed by a transmitter that can be seen as a voltage source (U) in series with a resistor (RI) where the resistor represents the transmitter impedance. If we assume that the transmitter is matched to the antenna (SWR 1:1) at resonance then RI is equal to RA.
The bandwidth of a short vertical monopole will depend on the antenna capacitance and resistance. A small capacitance will reduce the bandwidth and so will a low resistance (you cannot have it all ...). It is not wise to intentionally increase the (loss) resistance as this will reduce the antenna efficiency, but another advantage of a high capacitance (= large) antenna is an increased bandwidth.
The main concern is the current reduction and SWR increase then moving away from the resonance frequency. A short vertical monopole can be seen as a damped series resonance circuit, where C = antenna capacitance, L = loading coil inductance and R = loss resistance. At the resonance frequency L and C will cancel out each other and the impedance will be pure resistive (R). It is assumed that R is matched to the transmitter impedance (mostly 50 ).
).
Moving away from the resonance frequency will result in a reactive component is series with R, decreasing the antenna current and increasing the SWR. If the frequency offset from resonance is relatively small (few % only = anything within the 136kHz ham band) then the value of the reactive component can be given as :
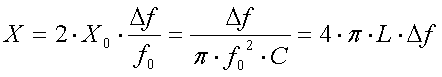 [19]
[19]
(X = reactance in  , fo = resonance frequency in Hz,
, fo = resonance frequency in Hz,  f = frequency offset from fo in Hz, Xo = reactance of C (or L) at resonance in
f = frequency offset from fo in Hz, Xo = reactance of C (or L) at resonance in  , C = antenna capacitance in F and L = loading coil inductance in H)
, C = antenna capacitance in F and L = loading coil inductance in H)
Example :
Assume we have an antenna with a capacitance of 300pF and a resistance of 60 . The antenna is brought to resonance at 137kHz.
. The antenna is brought to resonance at 137kHz.
At the lower band edge (135.7kHz) the reactive component X will be 74 , at the upper band edge (137.8kHz) it will be 45.5
, at the upper band edge (137.8kHz) it will be 45.5 .
.
Antenna current
The reactive component (X) of the antenna impedance will decrease the antenna current and thus the ERP. X can be calculated from formula 17.
We assume that the antenna is matched at resonance (X = 0, SWR = 1:1). If we move away from the resonance frequency the antenna will have a certain reactive component X and the antenna current will decrease to :
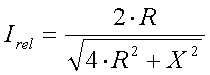 [20]
[20]
(Irel = antenna current relative to the current at resonance, R = antenna resistance in  and X = antenna reactance in
and X = antenna reactance in  )
)
Since the radiated power is proportional to the square of the antenna current it will be :
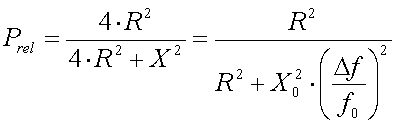 [21]
[21]
(Prel = radiated power relative to the power at resonance, R = antenna resistance in  , X = antenna reactance in
, X = antenna reactance in  , , Xo = untuned antenna reactance in
, , Xo = untuned antenna reactance in  ,
, 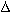 f = frequency offset from fo in Hz and f
f = frequency offset from fo in Hz and f
Example :
Assume we have an antenna with a capacitance of 300pF and a resistance of 60 . The antenna is brought to resonance at 137kHz and matched to the TX impedance at this frequency. The antenna current will decrease to 85% of the maximum current at the lower band edge (135.7kHz) and to 94% at the upper band edge (137.8kHz). The radiated power will decrease to 72% (-1.4dB) at the lower band edge and 87% (-0.6dB) at the upper band edge.
. The antenna is brought to resonance at 137kHz and matched to the TX impedance at this frequency. The antenna current will decrease to 85% of the maximum current at the lower band edge (135.7kHz) and to 94% at the upper band edge (137.8kHz). The radiated power will decrease to 72% (-1.4dB) at the lower band edge and 87% (-0.6dB) at the upper band edge.
The other way arround, if a certain power loss (Ploss) is acceptable the bandwidth (B) of the antenna system is :
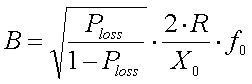 [22a]
[22a]
(B = bandwidth in Hz, Ploss = maximum acceptable power loss relative to the power at resonance, R = antenna resistance in  , X = antenna reactance in
, X = antenna reactance in  , Xo = untuned antenna reactance in
, Xo = untuned antenna reactance in  and f
and f
For 136kHz the bandwidth can be calculated from the maximum acceptable power loss, antenna resistance and antenna capacitance (or loading coil inductance) as :
 [22b]
[22b]
(B = bandwidth in Hz, Ploss = maximum acceptable power loss relative to the power at resonance, R = antenna resistance in  , C = antenna capacitance in pF and L = loading coil inductance in mH)
, C = antenna capacitance in pF and L = loading coil inductance in mH)
Example :
Assume we have an antenna with a capacitance of 300pF and a resistance of 60 . The antenna is brought to resonance at 137kHz and matched to the TX impedance at this frequency. If the acceptable power loss is 0.5dB then Ploss = 0.11. Based on formula 14 the antenna bandwidth will be 1.5kHz.
. The antenna is brought to resonance at 137kHz and matched to the TX impedance at this frequency. If the acceptable power loss is 0.5dB then Ploss = 0.11. Based on formula 14 the antenna bandwidth will be 1.5kHz.
Standing Wave Ratio (SWR)
Apart from decrease of the antenna current and radiated power a reactive component X will also increase the SWR.
Assuming that the SWR at resonance (X=0) is 1:1, a reactance X in series with R will increase the SWR to :
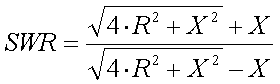 [23a] (R = resistance in
[23a] (R = resistance in  and X = reactance in
and X = reactance in  )
)
If the frequency offset is small, and thus the SWR is not too high, the formula can be simplified to :
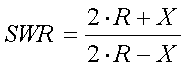 [23b] (R = antenna resistance in
[23b] (R = antenna resistance in  and X = antenna reactance in
and X = antenna reactance in  )
)
Formula 23b will have an accuracy of 10% or better if the outcome is an SWR of less than 3:1. For higher SWR it is recommended to use formula 23a.
For 136kHz the SWR can be directy calculated from 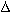 f, R and C (or L) as :
f, R and C (or L) as :
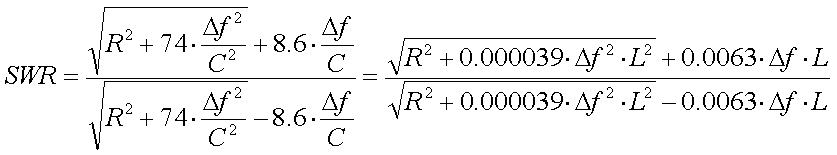 [23c]
[23c]
(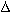 f = frequency offset from fo in Hz, R = antenna resistance in
f = frequency offset from fo in Hz, R = antenna resistance in  , C = antenna capacitance in pF and L = loading coil inductance in mH)
, C = antenna capacitance in pF and L = loading coil inductance in mH)
If the frequency offset is small, and thus the SWR is not too high, the formula can be simplified to :
 [23d]
[23d]
( f = frequency offset from fo in Hz, R = antenna resistance in
f = frequency offset from fo in Hz, R = antenna resistance in  , C = antenna capacitance in pF and L = loading coil inductance in mH)
, C = antenna capacitance in pF and L = loading coil inductance in mH)
Formula 23d will have an accuracy of 10% or better if the outcome is an SWR of less than 3:1, otherwise it is recommended to use formula 23c.
Example :
Assume we have an antenna with a capacitance of 300pF and a resistance of 60 . The antenna is brought to resonance at 137kHz and matched to the TX impedance at this frequency.
. The antenna is brought to resonance at 137kHz and matched to the TX impedance at this frequency.
If we use the simplified formula (23d) the SWR at the lower band edge (135.7kHz) is calculated as 4.2:1, at the upper band edge as 2.2:1. Since the SWR at the lower band edge is over 3:1 we have to recalculate is with formula 23c, the outcome is 3.2:1. For the higher band edge the outcome of formula 23c is 2.1:1.
As shown by this example the simplified formulas (23b and 23d) produce accetable results for an SWR less than 3:1. At high SWR they are not accurate, but this does not matter too much as an SWR of 3:1 or more just tells you that the antenna has to be better matched anyway.
So in most practical cases you can stick to the simplified formulas.
The bandwidth of an antenna, based on the maximum acceptable SWR, is :
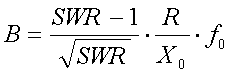 [24a]
[24a]
(B = bandwidth in Hz, R = antenna resistance in  , Xo = untuned antenna reactance in
, Xo = untuned antenna reactance in  and fo = resonance frequency in Hz)
and fo = resonance frequency in Hz)
For 136kHz the antenna bandwidth can be calculated from the acceptable SWR, antenna resistance and antenna capacitance (or loading coil inductance) as :
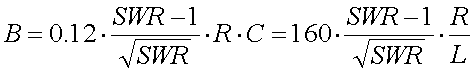 [24b]
[24b]
(B = bandwidth in Hz, R = antenna resistance in  , C = antenna capacitance in pF and L = loading coil inductance in mH)
, C = antenna capacitance in pF and L = loading coil inductance in mH)
Example :
Assume we have an antenna with a capacitance of 300pF and a resistance of 60 . The antenna is brought to resonance at 137kHz and matched to the TX impedance at this frequency. If a SWR up to 2:1 is acceptable the antenna bandwidth is 1.5kHz.
. The antenna is brought to resonance at 137kHz and matched to the TX impedance at this frequency. If a SWR up to 2:1 is acceptable the antenna bandwidth is 1.5kHz.
Relationship between SWR and power loss
If the SWR is known (measured) the power loss can be calculated as :
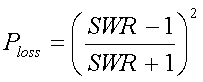 [25a]
[25a]
(Ploss = power loss relative to power at SWR 1:1)
The loss in dB is :
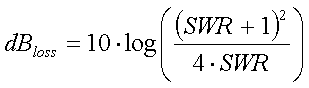 [25b]
[25b]
(Ploss = power loss relative to power at SWR 1:1 and log = 10 based logaritm)
Example :
A SWR of 1.7:1 will result in a 7% or 0.3dB power loss.
3.1. Antenna system
Under the term antenna system I mean more than just the antenna itself. It includes all surrounding parts that affect the radiation of the transmitter power : the transmission lines, matching devices and even enviroment.
3.2. Efficiency
If an antenna is fed with a certain power it will radiate a part of that power. The remaining part is dissipated 'uselessly', in most cases converted to heat in or arround the antenna. Simplified one can say that the transmitter feeds its power into 2 resistors, the radiation resistance (RA) and the loss resistance (RL).
The efficiency (n) of an antenna is :
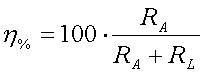 [26]
[26]
On HF the efficiency of most antenna systems is very high, 90% or more. The most important sources of loss are skin effect in the antenna wires and dissipation in the transmission line (coax cable). On VHF and higher frequencies these last can become very important.
On LF the situation is completely different, efficiencies of most antennas used by hams are in the range of 0.01 to 1%. The source of these high losses is dependent on the type of antenna. For electrical antennas the major losses will be mainly in the enviroment and the loading coil. For transmitting the efficiency of the antenna system will directly affect the amount of radiated power and thus is very important. But for receiving on LF it is mainly the ratio between wanted signal and unwanted signals (noise, QRM) that determines the quality of the antenna system. Therfore the efficiency is rather unimportant in a receiving antenna system.
3.3. Antenna system efficiency, antenna directivity, ERP, EIRP and EMRP
There is often a confusion between the terms efficiency and directivity or gain. While the efficiency is determined by the ratio of the transmitter power that is radiated, the directivity (often also called gain) is determined by the shape of radiation pattern. Even the term directivity is often only associated with directional antennas as Yagi's, Quads etc... But in practice any antenna has a certain gain, unless it radiates equally in all directions and under all angles. This 'gainless' antenna (that does not exist) is called a isotropic radiator and is taken as reference for the gain of other antennas (then the gain is given in dBi).
A 1/2 wave dipole has a gain of 2.15dBi and is often also taken as reference (then the gain is given in dBd).
Apart from the unchangable propagation parameters the signalstrength of a certain station on a certain frequency depends on the transmitter output power, the directivity of the antenna and the efficiency of the antenna system. These 3 parameters combined determine the radiated power, given in Watt.
Depending on the reference antenna there is :
Despite the fact that a short vertical antenna has a omnidirectional radiation pattern in the horizontal plane, it has a gain of 4.78dBi or 2.62dBd due to its directivity in the vertical plane. This gain is almost independent of the antenna height, as long as it it short compared to the wavelength (don't be fooled by the term short, at 136kHz it means 100m or less).
As the result of the different reference antennas EMRP will always be 2.62dB above ERP and 4.78dB above EIRP while ERP is always 2.17dB above EIRP.
Example :
Assume we feed a short vertical antenna with a radiation resistance of 0.04 and a loss resistance of 60
and a loss resistance of 60 with a power of 200W. The efficiency of the antenna system is 0.067% or -31.8dB (0.04/60). This means that from the 200W transmitter power there will be 133mW radiated (EMRP). As the gain of a short vertical is 2.62dBd (x 1.83) the ERP is 244mW. This means that the antenna system and transmitter as described here will produce the same signal strength as a power of 244mW sent into a perfect 1/2 wave dipole. The EIRP of this station will be 400mW
with a power of 200W. The efficiency of the antenna system is 0.067% or -31.8dB (0.04/60). This means that from the 200W transmitter power there will be 133mW radiated (EMRP). As the gain of a short vertical is 2.62dBd (x 1.83) the ERP is 244mW. This means that the antenna system and transmitter as described here will produce the same signal strength as a power of 244mW sent into a perfect 1/2 wave dipole. The EIRP of this station will be 400mW
3.4. Optimizing the antenna system efficiency
In order to improve the ERP of a LF station one can either increase the transmitter power or improve the antenna system efficiency. Although some dB's can be won by brute power the practical limit of increasing the transmitter power is often reached at 1-2kW. Any further improvement has to be done by optimizing the effeciency of the antenna system. This means increasing the radiation resistance of the antenna and/or decreasing the loss resistance.
The radiation resistance can be increased by making the antenna higher and adding capacitive and/or inductive toploading. A more complicated option is to implement multiple vertical elements.
The two most important components of the loss resistance are the losses in the loading coil and the ground/enviromental loss. The coil loss can be reduced by improving the coil's Q but indirectly also the capacitive topload will affect the coil loss, as for a larger antenna capacitance a smaller loading coil is needed. Depending on the value and Q of the loading coil, in most cases its loss resistance will be in the range of 5 to 20 .
.
The major component of the loss resistance is almost always the enviromental loss. It of often just called ground loss, although this last is only a part of the enviromental loss. The enviromantal loss is dependent of many factors such as soil type, objects near the antenna and even the shape and size of the antenna. In most cases it will be in the range of 30 to 150 .
.
3.5. Enviromental losses
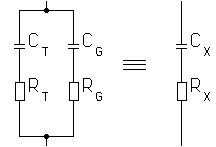
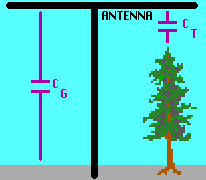
A short vertical antenna is capacitive coupled to its surrounding (the ground, trees, buildings, etc...). All of these surrounding objects also have a certain resistance that contributes to the enviromental loss of the antenna system. The RF current that is fed into the antenna seeks its way back via these capactive coupled objects and power is disipated in the resistances that these objects have.
The picture shows a simplified model : a T-antenna with a nearby tree. The antenna has capacitive coupling to the tree (CT) and to the ground (CG). Each of this 2 capacitances will form a return-path for the antenna current.
Example :
Assume that CT is 300pF and CG is 150pF. Further assume that the loss resistance of the tree (RT) is 200 and the loss resistance of the ground (RG) is 50
and the loss resistance of the ground (RG) is 50 .Finaly we assume that the antenna voltage is 5kV. The electrical model of this antenna system is shown right of the picture. Each return-path is represented by a capacitor in series with a resistor and we can calculate the impedance of each return-path : for a frequency of 136kHz the path via the tree is 3.9k
.Finaly we assume that the antenna voltage is 5kV. The electrical model of this antenna system is shown right of the picture. Each return-path is represented by a capacitor in series with a resistor and we can calculate the impedance of each return-path : for a frequency of 136kHz the path via the tree is 3.9k and the path via the ground is 7.8k
and the path via the ground is 7.8k . With an antenna voltage of 5kV this means that there is a current of 1.28A via the tree and a current of 0.64A via the ground.
. With an antenna voltage of 5kV this means that there is a current of 1.28A via the tree and a current of 0.64A via the ground.
Based on the values of CT, CG, RT and RG the total capacitance (CX) and enviromental loss resistance (RX) can be calculated : 450pF and 94 . At first glance it might look strange that RX is larger than RG. But this is due to the fact that in this example the capacitive coupling between the antenna and the tree (CT) is much larger than the capacitive coupling between antenna and ground (CG) and therefore RT contributes much more to RX than RG does. Notice that about 2/3 of the total antenna current is flowing back via CT and RT.
. At first glance it might look strange that RX is larger than RG. But this is due to the fact that in this example the capacitive coupling between the antenna and the tree (CT) is much larger than the capacitive coupling between antenna and ground (CG) and therefore RT contributes much more to RX than RG does. Notice that about 2/3 of the total antenna current is flowing back via CT and RT.
A very intersting experiment has been done in June 2007 by Jim Moritz (M0MBU) who measured the RF-current flowing through some trees near his 136kHz antenna (during transmission). Read his report:
It has often been said that trees surrounding an LF vertical antenna can be responsible for a substantial proportion of the antenna loss, and at my QTH there are several trees that have gradually been getting bigger over the
years, so I decided to try to measure how much RF current was actually flowing in some trees.
To measure the tree current, I used a Rogowski coil - this is like a toroidal RF current transformer, but without the magnetic core; instead of measuring the secondary current, the open-circuit voltage across the secondary is measured, and is proportional to the total current flowing through the area enclosed by the coil, the number of turns, the area of each turn, and the frequency. My Rogowski coil used 1.2m of rubber hose as a former, with about 500 turns of insulated wire, and had a scale factor of around 100mV out = 1A in. I measured the voltage with a SPM-3 selective voltmeter. The advantage of this type of current sensor is that the loop of flexible hose former can be made large enough to fit round a tree, and can be opened out, wrapped round the tree to be measured, and closed up again. A practical difficulty is that the output is quite small compared to a normal current transformer, and an aluminium foil electrostatic shield had to be added in order to reduce the effect of pick-up of the intense E-field directly under the antenna. This did not entirely eliminate the problem, but reduced it to a reasonable level.
I measured the current near ground level in the trunks of 8 trees - these are scattered around within about 10m horizontally of the antenna, with heights of about 5 to 10m (antenna height is around 9 to 11m). With an antenna current around 4A, the currents ranged from 50mA to 190mA, with the total for the 8 trees being 930mA. Generally, trees closer to the antenna and with bigger areas of foliage had higher currents, as you would expect.
The 8 measured are only a sample of the small trees and large bushes in and around my garden, also at about 20 to 40m distance there are larger trees all around my QTH as well. So it seems likely that a large fraction of the electric flux of the antenna is intercepted by a tree at some point, and a substantial proportion of the total antenna current is flowing to ground through trees. Since wood is a poor conductor, it is not surprising that trees close to the antenna increase the loss resistance. But also, current flowing vertically in the trees will contribute to the overall radiation of the antenna. However, since a current flowing "up" the antenna will be flowing "down" the tree, and the spacing of tree and antenna is a very small fraction of a wavelength, the effect of the tree current will be to partly cancel the overall radiation, and so reduce the radiation resistance. If the current flowing in the trees is a large fraction of the total antenna current, and the height of the trees is comparable with the antenna height, one could expect a substantial reduction in radiation resistance and effective height of the antenna, as the field strength measurements I made last week would seem to indicate.
The presence of objects such as trees and buildings near the antenna will have several effects :
 (if the ground would be the only return path) to 94
(if the ground would be the only return path) to 94 .
.
The increase of the enviromental loss resistance and decrease of the radiation resistance has a negative effect on the efficiency of the antenna system. The increased antenna capacitance has a positive effect, as you will need a smaller loading coil, but by no means it will compensate the negative effects.
3.6. Ground loss
On 'its way back' to the feeding point the antenna current flows (partly) through the ground. Since the soil is a rather poor conductor a loss resistance will be created.
The value of this loss resistance depends on :
3.6.1. Type (composition) of the soil
The ground loss is very dependent on the composition of the soil and is inverse related to the conductivity of the soil (the higher the conductivity the lesser the loss). Soil conductivity can be measured, but the results of these measurements should be taken with some caution for several reasons :
Typical soil conductivity :
| Soil type | Conductivity (mS/m) |
|---|---|
| salt water | 1000 |
| fresh water | 1 |
| wet soil | 1 - 10 |
| dry soil | 0.01 - 0.1 |
| meadow | 0.5 |
| loam | 8 - 20 |
| marsh | 30 - 60 |
| clay | 500 |
Soil conductivity can be improved by salting the soil, but due to the ecological impact this is not recommended (in many countries it is unlawfull). Also most fertilizers will improve the conductivity of the soil. Gypsum (calcium sulphate) is one of the best suited fertilizers, as it is relatively save to use and dissolves slowly (lasts a long time). Often (but not always) wet soil has a higher conductivity than dry soil. On LF the use of salt or excessive amounts of fertilizers will have little or no effect as this will only improve the conductivity in the upper layer of the soil while the LF signal penetrates deep into the ground. But longer periods of rain will wet the soil deep enough to affect the ground loss.
The signal radiated by the antenna penetrates in the ground. The deeper the signal penetrates the larger the ground loss will be. This penetration depth is inverse proportional to the square root of the of the soil conductivity. If the soil conductivity S is known the conduction depth D can be calculated (for 136kHz only) :
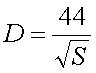 [27] (D in m and S in mS/m)
[27] (D in m and S in mS/m)
3.6.2. Frequency
The penetration depth of the signal in the ground is not only dependent of the soil conductivity but also of the frequency. In the LF and lower HF region (30kHz - 3MHz) the penetration depth is proportional to the square root of the wavelength (or otherwise said : inverse proportional to the square root of the frequency).
Based on the frequency F and the soil conductivity S the penetration depth D can be calculated :
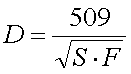 [28] (F in Hz, S in S/m and D in m)
[28] (F in Hz, S in S/m and D in m)
In most cases (and on 136kHz) the penetration depth will be between 40 and 150 metre, depending on the soil type. On salt water it will be only 1.5m.
Based on the above formula one could assume that the loss resistance will decrease with the square root of the frequency. But this will only be true if no other losses than ground loss are involved and if the soil has a uniform structure down to several tens (or even hunderds) metre deep. In practice the frequency dependency of the loss resistance will be different on any other location and might even change with the dimensions of the antenna. The first graph shows the results of the loss measurements done by M0BMU, ZL2CA and PA0SE on frequencies between 100 and 300kHz. The measurement data were fitted to a R = K1/FK2 function.
Other interesting measurements were done by Finbar O'Connor (EI0CF) and Alan Melia (G3NYK) who measured the loss resistance for different antenna configurations (at the QTH of EI0CF). These measurements show that even changing the antenna configuration can change the frequency dependency of the loss resistance, as the second graph shows.
3.6.3. Shape and dimensions of the antenna
Increasing height of a vertical antenna will increase the radiation resistance and thus the efficiency. But also increasing the topload will improve the efficiency. Apart from the fact that a larger topload creates a better current distribution several hams have also noticed that the loss resistance can significantly decrease when the topload covers a larger area.
Laurie Mayhead (G3AQC) has significantly improved his station by experimenting with different configurations of the topload and developed the "Footprint theory". Read his comments :
I started out with a 3 wire Marconi "T" antenna. This had a 30m top and a 15m vertical section, spacing between the top wires was 0.5m. I increased the spacing to 0.7m with no measurable difference in antenna current. The ground system was quite modest so I buried several hundred metres of wire with 10 earth rods at the ends of these radial wires. There was still very little increase in current, so I ran a 100m wire into the salt water and another 100m wire out to my 4 square array which has about 100 radials and a further 20 ground rods. Still no better. I was getting about 1.8A antenna current at the start and less than 2A at the finish. I measured 120 total loss resistance. Then I decided to change the top loading, although analysis with Eznec indicated no improvement. So the 3 top wires became a single wire not quite 3 times as long. There was no great change in capacitance (no change in the loading coil), but the current was now over 2.2A and the measured resistance 80
total loss resistance. Then I decided to change the top loading, although analysis with Eznec indicated no improvement. So the 3 top wires became a single wire not quite 3 times as long. There was no great change in capacitance (no change in the loading coil), but the current was now over 2.2A and the measured resistance 80 . Next I extended the top wires to 150m in a zig zag configuration because I didn't have the room to go in a straight line. I then got 3A and about 40
. Next I extended the top wires to 150m in a zig zag configuration because I didn't have the room to go in a straight line. I then got 3A and about 40 loss.Small improvements to my loading coil result in about 3.2A now.
loss.Small improvements to my loading coil result in about 3.2A now.
I think that there may have been a slight improvement because the aditional wire is further from the trees but I believe that the majority of the improvement is due to change in "current density" in the ground under the antenna. I call this my "Footprint theory". Basically its as if the antenna was a shower head and the ground a big bath with lots of outlets. Take the case of a basic vertical with no top load. The longer the vertical the higher the shower head and thus more outlets covered by the spray of water from the shower.Since each outlet can only get rid of a certain amount of water the more that are covered the more water gets away, the analogy is the lower the resistance! With an inverted-L or T ant the top wires are like several shower heads spaced out along the wire. So the longer the wire the more outlets recieving water.So its possible to bend the wire back on itself so long as the parts dont get too close. Alan Melia (G3NYK) commented that he visualised the fringing fields of a stripline over a conducting plane,he surmised that the effective width of the spray might be of the order of half the height of the wire. This would indicate that for maximum efficiency the normal parrallel top wires would need to be spaced by a distance equal to the height of the wires. I don't think that this is too far wrong.
In a recent mail to the reflector about the RUGBY 16kHz antenna it was mentioned that the original installation consisted of several multi wire cages,but that these were later replaced by a network of wires covering all the available ground area. This tends to support my Footprint theory and I would really like to find a reference to this work in the literature.
3.6.4. Radial system and ground rods
As mentioned before the antenna current 'returns' via the soil to the feeding point of the antenna. By adding a radial system and/or ground rod(s) the ground loss can be reduced.
The radial system contains a number of wires on or in the soil. As a general rule buried radials of bare wire are superior to radials on the ground or buried isolated radials. Burried radials should be at least 15cm (6 inch) deep in the soil. Although blank copper radials can be used, galvanized iron radials are cheaper and will be less affected by corrosion. The additional loss of iron radials (difference in conductivity between iron and copper) is almost always insignificant compared to the other losses.
Regarding the number of radials and their length the rule is simple : the more and the longer, the better. But there are some practical limits, once you have put a certain length of radials in the soils further extension of the radial system will only result in a marginal reduction of the ground loss.
In general the efficiency of a radial system is based on :
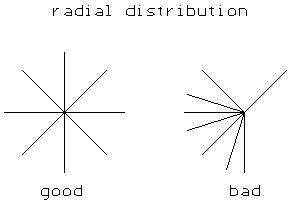
Best result are achieved when the radials are equally distributed over the area below the antenna (see left picture). Placing 2 radials too close is not very effective and will hardly bring any improvement over a single radial. Depending on the soil conductivity, radials need to be spaced at least 2m to 10m for optimal effect. When using many radials an optimized layout can reduce the ammount of wire needed (and the work to bury the radials) without loosing efficiency (see right picture).
In addition to radials, ground rods can reduce the ground loss. These rods can be located at the feeding point of the antenna or at the end of the radials, eventually also somewhere 'half way' the radials. Due to their relative small length it is essential that ground rods are blank metal. The longer (deeper) the ground rods are, the better. Getting the rods into the ground can be hard labour if you do it using a sledge hammer and brute force. If you don't have too much rock in the soil there is an easier way :
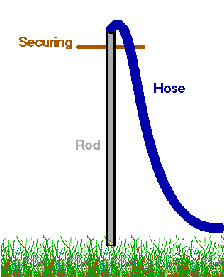
Use 1 inch galvanized iron tubing used for plumbing and often sold in practical 3m lengths. Connect your garden hose to one end of the tube and let the water flow trough the tubing. Hold the tube vertical on the soil, the water will wash the soil away and the tube will gently sink into the soil. Be aware that the tube can keep sinking into the soil even if you shut the water off, so it might be nessecary to secure the tube for some days to avoid a 'China syndrome'.
As so many things will influence the efficiency of a radial system (with or without ground rods) it is very difficult to predict how many radials and/or ground rods will give an optimal result in a particular case. The best way is to start with a limited number of radials / ground rods and gradually increase the ground system while measuring the loss resistance. That way you will find the point where further extension gives little or no improvement.
If you have problems to get long ground rods into the soil : one long rod can be replaced by some shorter rods, keeping the total length the same. In order to have maximum efficiency all rods should be separated by a distance that is at least their length (if possible twice their length).
I have found some result of research on the effect of the radials on the antenna efficiency in the long wave range. But this was in regard of commercial stations, where an efficiency of 80% was aimed. For a soil conductivity of 2mS, a wavelength of 2000m (150kHz) and an antenna length of less than 50m (170ft) the optimal length of a radial was found as 150m (500ft) and the optimal number of radials is 120. But I am afraid that only very few hams will have the possibilty to install such a radial system.
4.1. Electric field / magnetic field & near field / far field
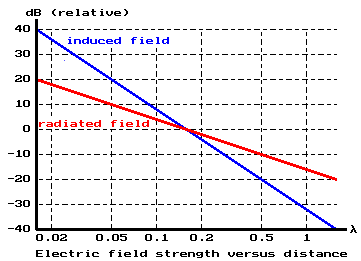
Despite the fact that some antennas are called electric antennas (eg. Marconi antenna) while others are called magnetic antennas (eg. small loop), any antenna will create both an electric and magnetic field.
Close to the antenna an electric antenna will have a strong electric field and a weak magnetic field. Moving away from the antenna the magnetic field will become stronger (relative to the electric field) and from a certain distance on the ratio between both fields will become constant. A magnetic antenna will have strong magnetic field and weak electric field near the antenna, but further away the electric field will become relatively stronger until the ratio both field again becomes constant. At this point both fields form together the electromagnetic field, they are coupled and cannot exist independently from each other.
Based on the above we can determine the :
Near field : area close to the antenna. The electric and magnetic fields are not coupled and the radio of their strength depends on the type of antenna and the distance from the antenna.
Far field : area at sufficiant distance from the antenna. The electric and magnetic fields are coupled and at a constant ratio.
Another way to look at it is to assume that any antenna will generate 2 kinds of fields, the induced field (that is dominant near the antenna) and the radiated field (that is dominant at a sufficiant distance). The induced field is much stronger at the antenna but declines much faster than the radiated field. The induced field just stores energy in the space arround the antenna (similar as a capacitor can store energy in an electric field or an inductor can store energy in a magnetic field) while the radiated field really radiates energy.
At a distance of about 0.16 wavelengths both fields will be equal and some sources let the far field start from here. But in practice it is recommended to respect a distance of at least 0.5 wavelengths for accurate fieldstrength measurements.
At a sufficiant distance from the antenna both fields will be in opposite polarization (so if the electric field is vertical the magnetic field will be horizontal), in phase and their ratio is determined by the free space impedance (377 ). This means that one can determine the magnetic field if the electric field is known and vice versa, so it is of no importance wether the measurements are done with a small whip or a loop (ferrite rod).
). This means that one can determine the magnetic field if the electric field is known and vice versa, so it is of no importance wether the measurements are done with a small whip or a loop (ferrite rod).
4.2. Calculated ERP versus ERP measurements
A few hams have actually measured their ERP, the results are in the table below :
It is remarkable that in all cases the measured ERP is below the calculated ERP, differences going from 1 to more than 5dB. In the fall of 2001 Jim Moritz (M0BMU) has done over 200 ERP measurements at distances of a few 100m up to 8km from the antenna. In addition Jim has measured the ERP of 2 antennas subsequently placed at the same location, a 8m high inverted-L and a 17.5m high umbrella (inverted-V) antenna. These measurements show that the measured ERP is relatively constant from a distance of 1km upward, so the origin of the extra loss is in the direct environement of the antenna. Further the 17.5m high antenna seems to suffer less from this loss than the 8.5m high antenna, this may indicate that this extra loss is caused by objects near to the antenna and that this loss is dependent of the radio of the antenna height versus the dimensions of these objects (thus a bigger antenna suffering less from this loss).
Finaly the measurements confirm that the distance to the antenna has to be at least 1km (+/- 0.5 wavelenght), if possible at 2km (+/- 1 wavelength) or more, in order to get meaningfull results :
4.3. How to measure ERP
The ERP is determined by measuring the fieldstrength E at a known distance d from the antenna :
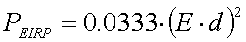 [29] (PEIRP in W, E in mV/m and d in km)
[29] (PEIRP in W, E in mV/m and d in km)
Remember that you need to divide the EIRP by 1.64 (or subtract 2.15dB) to get the ERP.
Measuring ERP is not very complicated, but one should keep a few things in mind :

For practical reasons a small loop or ferrite rod antenna is best suited for ERP measurements. First of all a magnetic antenna is less sensible to the environement (compared to a small whip) and also it is easier to calibrate. The calibration is done by creating a known magnetic field, using a pair of Helmholtz coils (see picture). Be aware that is in the combination of antenna and receiver that has to be calibrated.
A detailed procedure how to perform fieldstrength measurements is described by Dick Rollema (PA0SE), have a look here. It includes the construction of a simple measurement receiver, the pair of Helmholtz coils and the calibration procedure.
More interesting reading on fieldstrength measurements on LF, by Christer Andersson (SM6PXJ), can be found here.
5.1. Single turn small loop as transmitting antenna
In this chapter the small loop antenna will be discussed as a transmitting antenna. For receiving-only small loop antennas I refer to chapter 7. For simplicity we will start with a single turn loop.
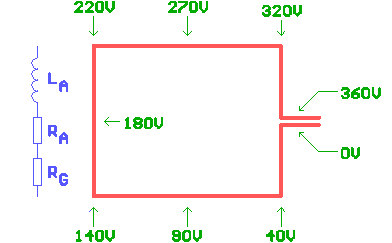
Assume we have a single turn loop antenna with an area A. If the loop dimensions are small compared to the wavelength then :
As for any other small antenna the ERP is mainly determined by the ratio of the radiation resistance to the loss resistance (apart from the TX power of course). Only in second order the antenna directivity (gain) will play a role. So the basic rule "the bigger the better" is also valid for small loops.
The radiation resistance RA of a single turn small loop antenna with an area A and at a wavelength 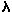 is :
is :
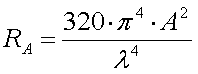 [30a]
[30a]
For 136kHz this is :
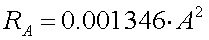 [30b] (RA in µ
[30b] (RA in µ and A in m2)
and A in m2)
The radiation resistance depends on the loop area, not on the loop shape. This means that a 20m high and 20m long loop will have the same radiation resistance as a 8m high and 50m long loop (both are 400m2). But the 20m x 20m loop will require only 80m wire while the 8m x 50m loop needs 116m. As a result copper losses in the square loop (20m x 20m) will be 45% less than these in the rectangular loop (8m x 50m).
Although a square loop will have a better efficiency than a rectangular loop with the same area (and a circular loop would even be better than a square), practical limitations will often make a rectangular loop the best solution.
The inductance of a loop depends on the shape, dimensions and wire diameter :
 [31a]
[31a]
(LA = loop inductance in µH, P = loop perimeter (circumreference) in m, A = loop area in m2, d = wire diameter in mm and ln = natural logaritm)
(This formula was derived by Claudio Girardi (IN3OTD) from a general formula for the inductance of a single turn loop proposed by Bashenoff in 1928. The accuracy is within a few % for the most common loop shapes.)
A more specific formula for rectangular loops derived by Alexander Yurkov (RA9MB) is :
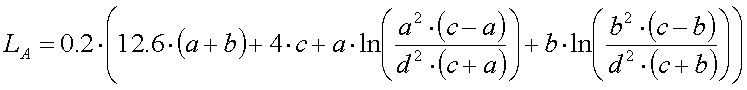 [31b]
[31b]
(LA = loop inductance in µH, a / b = height / length of the loop in m, d = wire diameter in mm, ln = natural logaritm and
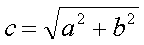 )
)
The 3 main components of the loss resistance (RL) are :
The wire loss depends on the length, diameter and composition of the loop wire. Due to the skin-effect it often is better to use several thin wires in parallel than a single thick wire. For those who can afford it litz-wire is the best choise.
Since a small loop is inductive the matching network to bring the antenna to resonance (and eventually match it to 50 ) is capacitive. Choosing the right types, the Q-factor of the capacitors can be very high (up to 1000 and more) and thus the loss in the matching network can be kept low. But keep in mind that the radiation resistance of a loop is in the µ
) is capacitive. Choosing the right types, the Q-factor of the capacitors can be very high (up to 1000 and more) and thus the loss in the matching network can be kept low. But keep in mind that the radiation resistance of a loop is in the µ range, so even a few m
range, so even a few m of loss can cause a significant degradation of the antenna efficiency.
of loss can cause a significant degradation of the antenna efficiency.
Even though a small loop antenna is much less sensitive to the enviroment than a short vertical antenna the enviromental loss is still important. The best way to reduce this loss low is to keep all wire as far away as possible from the ground and surrounding objects.
5.2. Efficiency of a loop
The efficiency of an antenna is determined by the ratio of the radiation resistance (RA) to the loss restistance (RL) :
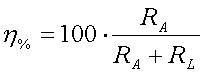 [32]
[32]
For a small loop antenna the efficiency will be very low, typical far less than 1%. So by measuring the RF resistance of a small loop you will be able to determine the loss restistance. The radiation resistance can be calculated using formula 30 and thus the efficiency can be determined.
Example :
Assume you have a rectangular loop of 15m high and 30m long. This loop has an area of 450m2 and a perimeter of 90m. Based on formula 30 the radiation resistance is 270µ . Further assume that the AC resistance of the loop wire is 0.5
. Further assume that the AC resistance of the loop wire is 0.5 (based on copper wire of 5mm diameter), the loss in the matching device is 0.1
(based on copper wire of 5mm diameter), the loss in the matching device is 0.1 and the enviromental loss is 1.5
and the enviromental loss is 1.5 . The total loss resistance is 0.5 + 0.1 + 1.5 = 2.1
. The total loss resistance is 0.5 + 0.1 + 1.5 = 2.1 . With a radiation resistance of 270µ
. With a radiation resistance of 270µ the efficiency will be 0.013% or -39dB.
the efficiency will be 0.013% or -39dB.
A giant loop of 25m high and 100m long, using 10mm diameter copper wire, will have an efficiency of -31dB or 0.07% (0.008 radiation resistance versus 11
radiation resistance versus 11 loss).
loss).
5.3. Enviromental losses of small loop antennas
under  construction
construction
5.4. Single turn loop versus multi turn loop
under  construction
construction
5.5. Directivity and polarization of a small loop antenna
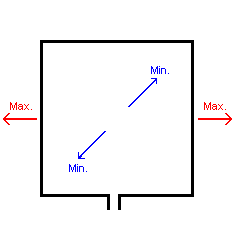
Directivity
In contradiction to a vertical antenna the small loop antenna is not omnidirectional in the horizontal plane. It has a kind of 8-shaped horizontal radiation pattern with a 3dB opening angle of 90°. The nulls are in theory infinite if the loop would be completely insensitive to the electric field. But in practice most transmitting loops are not shielded and thus will pick up some of the electric field. As a result practical values for the loop nulls are -20 to -30dB.
Keep in mind that the maxima of the horizontal radiation pattern are on the plane of the loop while the minima are orthogonal to the loop plane. As long as the loop dimensions do not exceed a wavelength the radiation pattern does not depend on the loop size.
The gain of a small loop antenna is 1.76dBi or -0.39dBd. Dispite the fact that a loop antenna has some horizontal directivity its gain is less than that of a short vertical antenna (4.77dBi or 2.62dBd). This is caused by the fact that a short vertical antenna has more directivity in the vertical plane.
Example :
Assume a rectangular loop of 15 by 30m as described in the previous example. The total loss resistance of this loop is 2.1 , while the radiation resistance is 270µ
, while the radiation resistance is 270µ . If we connect a 100W TX (and perform perfect impedance matching) the antenna current will be 6.9A and the radiated power thus will 13 milli-Watt. The EIRP is 19mW, the ERP is 12mW
. If we connect a 100W TX (and perform perfect impedance matching) the antenna current will be 6.9A and the radiated power thus will 13 milli-Watt. The EIRP is 19mW, the ERP is 12mW
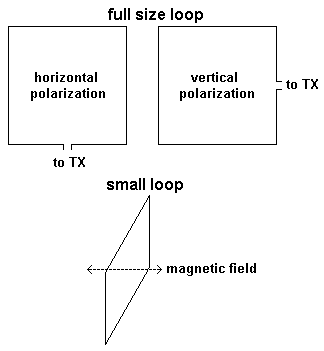 The giant loop of 25 by 100m had a Rloss of 11
The giant loop of 25 by 100m had a Rloss of 11 and a Rrad of 0.008
and a Rrad of 0.008 . Putting 100W into this will will cause an Iant of 3A and a Prad of 73 milli-Watt. In this case the EIRP is 109mW, the ERP is 66mW.
. Putting 100W into this will will cause an Iant of 3A and a Prad of 73 milli-Watt. In this case the EIRP is 109mW, the ERP is 66mW.
Polarization
A full size loop antenna in the vertical plane can be horizontal or vertical polarized (see picture at the right). This is because the current distribution over the antenna is not uniform.
At LF however the antenna dimensions are small (compared to the wavelength). As a consequence the current is constant over the entire antenna, what means that the polarization of a small loop antenna must be independent of the location of the feeding point.
One way to approach this is to assume that a small loop antenna acts similar to a coil : the current is constant thoughout the coil/loop and the voltage is built up over the coil/loop. For a coil it is known that it generates a magnetic field in right angles to the plane of the winding(s). Thus for a vertical oriented small loop the magnetic field is horizontal. Further we know that the electric field of an antenna must be orthogonal to the magnetic field, thus the electric field is vertical. Since the antenna polarization is always reffering to the plane of the electric field a small loop antenna - in the vertical plane - will always be vertical polarized, regardless of where it is fed.
5.6. Bringing a small loop antenna to resonance
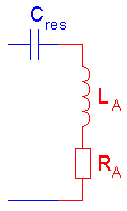
5.6.1. Resonance capacitor A small loop antenna can be seen as an inductance (LA)in series with a resistor (RA). The inductance depends on the loop dimemsions (see here) while the resistance in mainly determined by the losses.
The antenna is brought to resonance by a series capacitor (Cres in F) :
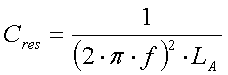 [33a]
[33a]
(LA = loop inductance in H and f = frequency in Hz)
For 136kHz Cres can be calculated as :
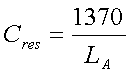 [33b]
[33b]
(Cres = resonance capacitor in nF and LA = loop inductance in µH)
At resonance the inductive and capacitive reactances will cancel out each other and the resulting impedance will be resistive and equal to RA.
5.6.2. Impedance matching
Once the loop is brought to resonance the impedance is resistive but probably still different from the transmitter impedance. A typical loop resistance is in the range of 0.5 to 5 while the TX impedance often is 50
while the TX impedance often is 50 , so we will have rather high transformation ratios (1/10 to 1/100, whereas a typical transformation ratio for a short vertical monopole is only in the order of 1/1 to 1/3).
, so we will have rather high transformation ratios (1/10 to 1/100, whereas a typical transformation ratio for a short vertical monopole is only in the order of 1/1 to 1/3).
Impedance matching can either be done using a transformer or using a variant on the L-C network (in fact we will need a C-C network).
Transformer
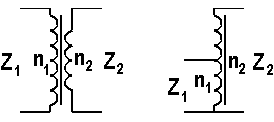 Impedance matching can be done using a transformer, either a isolating or a non-isolating one (auto-transformer) :
Impedance matching can be done using a transformer, either a isolating or a non-isolating one (auto-transformer) :
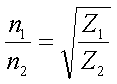 [34] (Z1 ... Z2 = impedances , n1 ... n2 = turns)
[34] (Z1 ... Z2 = impedances , n1 ... n2 = turns)
Example :
We want to match a 1.5 antenna to our 50
antenna to our 50 transmitter. That means that the ratio of the turns has to be 5.77. With n1 = 23 and n2 = 4 we come close to this value.
transmitter. That means that the ratio of the turns has to be 5.77. With n1 = 23 and n2 = 4 we come close to this value.
Details on impedance matching with a transformer were given when the matching of short vertical monopoles was discussed (see here). More about the design of a transformer and the selection of care material can be found here.
As the transformer ratio is rather large the choise of the right material to make a transformer for a small loop antenna can be more critical than for a short vertical monopole.
C-C network
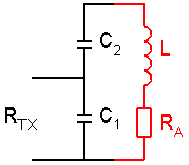 A simple C-C network can be used for impedance transformation :
A simple C-C network can be used for impedance transformation :
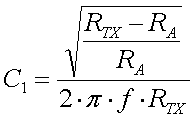 [35a]
[35a]
and
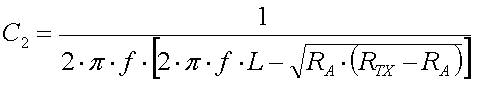 [35b]
[35b]
(L = antenna inductance in H, C1 ... C2 = capacitances in F, RA antenna resistance in  , RTX = transmitter impedance in
, RTX = transmitter impedance in  and f = frequency in Hz)
and f = frequency in Hz)
For a frequency of 136kHz C1 and C2 can be calculated as :
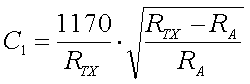 [35c]
[35c]
and
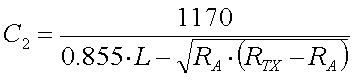 [35d]
[35d]
(L = antenna inductance in µH, C1 ... C2 = capacitances in nF and RA antenna resistance in  and RTX = transmitter impedance in
and RTX = transmitter impedance in  )
)
Example :
We want to match a small loop with an inductance of 70µH and a resistance of 0.65 to our 50
to our 50 transmitter. Based on formula 35 C1 = 204nF and C2 = 21.6nF.
transmitter. Based on formula 35 C1 = 204nF and C2 = 21.6nF.
One should take care to choose the right capacitors. Most ceramic and metalfilm capacitors will have too much loss on LF. Capacitors that can be used are :
Be aware that - using high power - currents of several 10A can flow through the capacitors. Eventually it can be usefull to use several capacitors in parallel.
5.6.3. Bandwidth considerations
under  construction
construction
under  construction
construction
under  construction
construction
9.1 High power applications of toroidal core coils
9.1.1. About toroidal cores Using toroidal cores one can make coils that are compact and have little stray field. These properties make toroids popular for the design of transformers and for inductances in impedance matching and filter circuits. The inductance (L) of a toroidal core coil can easily be calculated based on the material specific inductance factor (AL) :
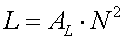 [36]
[36]
(L in nH, AL in nH/turn2, N = number of turns)
Sometimes AL is expressed in µH / 100turns, the conversion to nH/turn2 is : 1 µH / 100 turns = 0.1 nH/turn2.
The power that can be handled by a toroidal core is limited by 2 factors : saturation of the core material and temperature rise of the core.
Material saturation
At low currents the magnetic flux in a core will be proportional to the current through the coil and the inductance will be constant (independent of current or flux). But if the current exceeds a certain value the magnetic flux will no longer increase proportional to the current and the inducance will drop. This is called saturation and it will cause a distortion of the signal.
To make things worse, the inductance drop will also cause the reactance to drop and thus the current will increase. This will cause a further inductance drop etc... , a nice example of a chain reaction.
So, at any time saturation of the core material should be avoided.
The peak flux density in the core is given by :
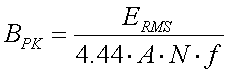 [37]
[37]
(Bpk = flux in T, ERMS = applied voltage in VRMS, A = effective cross-sectional area in m2, N = number of turns and f = frequency in Hz)
The flux should not exceed 0.2 to 0.25T for ferrite materials and 1 to 1.2T for iron powder.
Temperature rise
The temperature rise of the core is caused by permeability losses in the core and the copper losses in the wire :
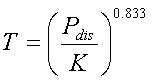 [38]
[38]
(T = temperature rise in °C or K, Pdis = total power dissipation in mW and K = core surface area in cm2)
The above formula is an approximation for a core in free standing air. Temperature rise can be decreased if a forced air cooling (fan) is used.
Core material : iron powder versus ferrite
For typical high power RF applications ferrite cores will be limited by saturation while iron powder cores will be limited by temperature rise. Further a ferrite core will have a 100-200 times higher AL compared to an iron powder core of the same dimensions (and thus needs 10 to 15 times less turns for the same inductance).
In general can be said that, at LF, ferrite is best suited for wideband applications such as transformers and baluns while iron powder is prefered for high-Q applications such as resonant circuits, low-pass filters and L-C impedance matching circuits. In principle one could use iron powder also for wideband applications, but the number of turns needed is often impracticable high.
9.1.2. Designing a ferrite cored transformer (by Jim Moritz, M0BMU)
Some maths is needed to design a ferrite cored transformer.
The first stage is to chose a number of turns that can withstand the applied voltage without saturating the core. You need to choose the number or turns (N) so that peak flux density (Bpk) is less than about 0.2 to 0.25T for most power ferrites (formula 37).
You also need to ensure the inductance of the transformer is high enough, usually so that the reactance is at least 5 times the impedance level :
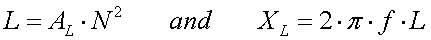 [39]
[39]
(AL = the material specific inductance factor, usually in nH/turn2, L = inductance in the same units as AL, N = number of turns, XL = reactance in Ohm and f = frequency in Hz)
If AL is not known, it can be calculated from :
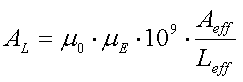 [40]
[40]
(AL in nH/turn2, µ0 = permeability of free space (4* *10-7), µE = effective permeability (usually about 2000 for power ferrites), Leff = effective magnetic path length in m and Aeff = effective cross-sectional area in m2)
*10-7), µE = effective permeability (usually about 2000 for power ferrites), Leff = effective magnetic path length in m and Aeff = effective cross-sectional area in m2)
Or you could wind some turns on the core and measure the inductance.
The parameters µE, Leff and Aeff have to be retrieved from the manufacturers data sheet, eventually Leff and Aeff can be determined from the core dimensions, if you can accept an error of a few %.
Example :
Assume we have a core with an inner diameter of 30mm, an outer diameter of 46mm and a height of 12mm.
The average diameter is 38mm [(30+46)/2], so Leff =  *38 = 119.4mm.
*38 = 119.4mm.
The inner diameter is 15mm [30/2] and the outer diameter is 23mm [46/2], Aeff = (outer diameter - inner diameter) * height = 96mm2 [(23-15)*12]. Due to the rounded egdes Aeff will be slightly less, but in most cases the error is acceptable.
There is also core losses to be taken into account and the temperature rise these produce, but this is more complicated to work out and requires the manufacturer's data. And for ferrite cores generally saturation will occur before the critical temerature rise is reached. Using a generously sized core to start with usually means the transformer will run cool. You should choose wire sizes that fill up the available winding space, to minimise resistive losses.
As a few examples of LF TX power applications for ferrite cores, I have used :
All these components run at a comfortable temperatures without additional cooling at the given power level.
The 3C8, 3C80, 3C85, 3C90 materials are manganese-zinc ferrite of a type that seems to be ubiquitous for switch-mode designs. The Neosid F44 and Siemens N27, N67, and N87 grades are very similar - the higher numbers represent newer materials with slightly improved performance, but the differences are not great. Most ferrite manufacturers seem to make something very similar. These all seem to work well as transformers at 136k. There are newer materials around like 3F3, but the availability seems to be very limited.
In general, transformers require maximum inductance with minimum turns, so no air gap is used. For maximum energy storage with minimum losses in a resonant application, or for a choke with a large DC current component, an air gap is required. Power types of ferrites can be used with an air-gap to produce inductors for resonant or filtering applications, but it seems to be difficult to get a Q of more than about 100 or so; The micrometals -2 mix iron dust cores seem to be better in this application. The iron dust cores made for SMPSU applications also seem to have relatively high losses at 136k. For small-signal applications, the nickel-zinc HF ferrites like 4C65 seem to be capable of very high Q, but are not particularly suited to LF power applications, and are not very widely available. They usually have much lower permeability, 100 or so. The manganese-zinc ferrite, gapped pot cores with tuning slugs (eg RM series) seem to give a Q between 100 - 200 at LF for low-level filter applications.
The ferrites designed for RFI supression seem to have high losses over a wide frequency range (which is what they are designed for , of course), so not very good for signal processing. The very high permeability manganese zinc ferrites for signal transformers tend also to have higher losses, and need to operate at lower Bpk.
Surplus ferrites can sometimes be used. for example, line-output transformer cores in video monitors are usually a 3C8-type material. But be careful to clean the mating surfaces so they are a close fit, and remove any plastic film spacers, etc. 3C8 and 3C85 etc. toroids usually have a red or pink coating. 4C65 has a purple coating. The rough surface of low frequency manganese-zinc ferrites usually has a fairly shiny, glazed appearance, whereas nickel-zinc ferrite has a more matt grey appearance. Ferrites are very hard and brittle, while iron dust materials can easily be cut with a file. There are also various powdered metal cores, which look metallic when the coating is removed, but these do not seem to work well at 136k.
9.1.3. Designing an iron powder cored coil Where for ferrite material the saturation will be the limiting factor, for iron powder it will be the temperature rise in the core. This temperature rise is caused by the power dissipation, as given in formula 38. The core loss is determinded by the material, the frequency and the flux density. For most iron powder materials the core loss will rise more or less proportional with the frequency and with the square of the flux density.
To give one example, for the popular '#2' material (red) that is available from several manufacturers :
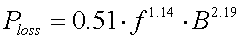 [41]
[41]
(Ploss core loss in mW/cm3, f = frequency in Hz and B = flux density in T)
Since the surface area of a toroid core is approximately proportional to the square of the core diameter, while the volume is proportional to the cube of the diameter, a smaller diameter core can dissipate more power per volume unit. As a result it can be usefull (and cost efficient) to put 2 smaller coils in series instead of one large coil.
My thanks go to :